جيب التمام 30 حسب جدول براديس. جيب التمام (sin x) وجيب التمام (cos x) - الخصائص والرسوم البيانية والصيغ

جدول الدوال المثلثية الأساسية للزوايا 0، 30، 45، 60، 90، ... درجات

من التعريفات المثلثية للدوال $\sin$ و $\cos$ و $\tan$ و $\cot$، يمكنك معرفة قيمها للزوايا $0$ و $90$ درجة:

$\sin⁡0°=0$، $\cos0°=1$، $\tan 0°=0$، $\cot 0°$ غير محدد؛

$\sin90°=1$، $\cos90°=0$، $\cot90°=0$، $\tan 90°$ غير محدد.

في دورة الهندسة المدرسية، عند دراسة المثلثات القائمة، يجدون الدوال المثلثية للزوايا $0°$، $30°$، $45°$، $60°$، $90°$.

تم العثور على قيم الدوال المثلثية للزوايا المشار إليها بالدرجات والراديان، على التوالي ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) لسهولة الحفظ والاستخدام يتم إدخالها في جدول يسمى الجدول المثلثي, جدول القيم الأساسية للدوال المثلثيةوما إلى ذلك وهلم جرا.

عند استخدام صيغ التخفيض، يمكن توسيع الجدول المثلثي إلى زاوية $360°$، وبالتالي $2\pi$ راديان:

باستخدام الخصائص الدورية للدوال المثلثية، يمكن حساب وتسجيل كل زاوية، والتي ستختلف عن الزاوية المعروفة بالفعل بمقدار $360°$، في جدول. على سبيل المثال، الدالة المثلثية للزاوية $0°$ سيكون لها نفس القيمة للزاوية $0°+360°$، وللزاوية $0°+2 \cdot 360°$، وللزاوية $0°+3 \cdot 360°$ وإلخ.

باستخدام جدول المثلثات، يمكنك تحديد قيم جميع زوايا دائرة الوحدة.

في دورة الهندسة المدرسية، من المفترض أن تحفظ القيم الأساسية للدوال المثلثية المجمعة في جدول مثلثي لتسهيل حل المسائل المثلثية.

باستخدام الجدول

يكفي في الجدول العثور على الدالة المثلثية المطلوبة وقيمة الزاوية أو الراديان التي يجب حساب هذه الدالة من أجلها. عند تقاطع الصف مع الوظيفة والعمود مع القيمة، نحصل على القيمة المطلوبة للدالة المثلثية للوسيطة المحددة.

في الشكل، يمكنك معرفة كيفية العثور على قيمة $\cos⁡60°$، والتي تساوي $\frac(1)(2)$.

يتم استخدام الجدول المثلثي الممتد بنفس الطريقة. وميزة استخدامه، كما ذكرنا سابقًا، هي حساب الدالة المثلثية لأي زاوية تقريبًا. على سبيل المثال، يمكنك بسهولة العثور على القيمة $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$:

جداول براديس للدوال المثلثية الأساسية

يتم توفير القدرة على حساب الدالة المثلثية لأي قيمة زاوية على الإطلاق لقيمة عدد صحيح من الدرجات وقيمة عدد صحيح من الدقائق من خلال استخدام جداول Bradis. على سبيل المثال، ابحث عن قيمة $\cos⁡34°7"$. يتم تقسيم الجداول إلى جزأين: جدول قيم $\sin$ و$\cos$ وجدول قيم $ \tan$ و$\cot$.

تتيح جداول Bradis الحصول على قيم تقريبية للدوال المثلثية بدقة تصل إلى 4 منازل عشرية.

استخدام جداول براديس

باستخدام جداول براديس للجيب، نجد $\sin⁡17°42"$. للقيام بذلك، في العمود الأيسر من جدول الجيب وجيب التمام نجد قيمة الدرجات - $17°$، وفي السطر العلوي نجد قيمة الدقائق - $42"$. عند تقاطعهم نحصل على القيمة المطلوبة:

$\sin17°42"=0.304$.

للعثور على القيمة $\sin17°44"$ تحتاج إلى استخدام التصحيح على الجانب الأيمن من الجدول. في هذه الحالة، إلى القيمة $42"$ الموجودة في الجدول، تحتاج إلى إضافة تصحيح بقيمة $2 "$، وهو ما يعادل $0.0006$. نحصل على:

$\sin17°44"=0.304+0.0006=0.3046$.

للعثور على القيمة $\sin17°47"$ نستخدم أيضًا التصحيح على الجانب الأيمن من الجدول، فقط في هذه الحالة نأخذ القيمة $\sin17°48"$ كأساس ونطرح التصحيح لـ $1"$ :

$\sin17°47"=0.3057-0.0003=0.3054$.

عند حساب جيب التمام، نقوم بإجراءات مماثلة، لكننا ننظر إلى الدرجات في العمود الأيمن، والدقائق في العمود السفلي من الجدول. على سبيل المثال، $\cos20°=0.9397$.

لا توجد تصحيحات لقيم الظل حتى $90°$ وظل التمام ذو الزاوية الصغيرة. على سبيل المثال، لنجد $\tan 78°37"$، والتي وفقًا للجدول تساوي $4.967$.

جدول قيم الدوال المثلثية

يتم تجميع جدول قيم الدوال المثلثية للزوايا 0 و30 و45 و60 و90 و180 و270 و360 درجة وقيم الزوايا المقابلة بالراديان. من بين الدوال المثلثية، يوضح الجدول الجيب وجيب التمام والظل وظل التمام والقاطع وقاطع التمام. ولتسهيل حل الأمثلة المدرسية، يتم كتابة قيم الدوال المثلثية في الجدول على شكل كسر مع الحفاظ على علامات استخراج الجذر التربيعي للأعداد، مما يساعد في كثير من الأحيان على تقليل التعبيرات الرياضية المعقدة. بالنسبة للظل وظل التمام، لا يمكن تحديد قيم بعض الزوايا. بالنسبة لقيم الظل وظل التمام لهذه الزوايا، توجد شرطة في جدول قيم الدوال المثلثية. ومن المقبول عمومًا أن ظل وظل التمام لهذه الزوايا يساوي اللانهاية. توجد في صفحة منفصلة صيغ لتقليل الدوال المثلثية.

يوضح جدول قيم دالة الجيب المثلثية قيم الزوايا التالية: sin 0، sin 30، sin 45، sin 60، sin 90، sin 180، sin 270، sin 360 بالدرجات، وهو ما يتوافق مع الخطيئة 0 بي، الخطيئة بي / 6، الخطيئة بي / 4، الخطيئة بي / 3، الخطيئة بي / 2، الخطيئة بي، الخطيئة 3 بي / 2، الخطيئة 2 بي في راديان قياس الزوايا. الجدول المدرسي للجيوب.

بالنسبة لدالة جيب التمام المثلثية، يوضح الجدول قيم الزوايا التالية: cos 0، cos 30، cos 45، cos 60، cos 90، cos 180، cos 270، cos 360 بالدرجات، وهو ما يتوافق مع cos 0 pi ، cos pi على 6، cos pi على 4، cos pi على 3، cos pi على 2، cos pi، cos 3 pi على 2، cos 2 pi بقياس راديان للزوايا. الجدول المدرسي لجيب التمام.

يعطي الجدول المثلثي لدالة الظل المثلثية قيمًا للزوايا التالية: tg 0، tg 30، tg 45، tg 60، tg 180، tg 360 في قياس الدرجة، وهو ما يتوافق مع tg 0 pi، tg pi/6، tg pi/4، tg pi/3، tg pi، tg 2 pi في قياس راديان للزوايا. لم يتم تعريف القيم التالية لدوال الظل المثلثية tan 90، tan 270، tan pi/2، tan 3 pi/2 وتعتبر مساوية لما لا نهاية.

بالنسبة للدالة المثلثية ظل التمام في الجدول المثلثي، يتم إعطاء قيم الزوايا التالية: ctg 30، ctg 45، ctg 60، ctg 90، ctg 270 في قياس الدرجة، وهو ما يتوافق مع ctg pi/6، ctg pi/4 ، ctg pi/3، tg pi/ 2، tan 3 pi/2 بقياس راديان للزوايا. لم يتم تعريف القيم التالية لدوال ظل التمام المثلثية ctg 0، ctg 180، ctg 360، ctg 0 pi، ctg pi، ctg 2 pi وتعتبر مساوية لما لا نهاية.

يتم إعطاء قيم الدوال المثلثية القاطعة وقاطعة التمام لنفس الزوايا بالدرجات والراديان مثل الجيب وجيب التمام والظل وظل التمام.

يوضح جدول قيم الدوال المثلثية للزوايا غير القياسية قيم الجيب وجيب التمام والظل وظل التمام للزوايا بالدرجات 15، 18، 22.5، 36، 54، 67.5 72 درجة وبالراديان pi/12 ، بي/10، بي/ 8، بي/5، 3بي/8، 2بي/5 راديان. يتم التعبير عن قيم الدوال المثلثية من حيث الكسور والجذور التربيعية لتسهيل تبسيط الكسور في الأمثلة المدرسية.

ثلاثة وحوش أخرى في علم المثلثات. الأول هو ظل 1.5 درجة ونصف أو باي مقسومًا على 120. والثاني هو جيب تمام باي مقسومًا على 240، باي/240. الأطول هو جيب تمام pi مقسومًا على 17، pi/17.

تمثل الدائرة المثلثية لقيم وظائف الجيب وجيب التمام بصريًا علامات الجيب وجيب التمام اعتمادًا على حجم الزاوية. خاصة بالنسبة للشقراوات، يتم وضع خط تحت قيم جيب التمام بشرطة خضراء لتقليل الارتباك. يتم أيضًا عرض تحويل الدرجات إلى الراديان بشكل واضح جدًا عند التعبير عن الراديان بدلالة pi.

يعرض هذا الجدول المثلثي قيم الجيب وجيب التمام والظل وظل التمام للزوايا من 0 صفر إلى 90 درجة على فترات من درجة واحدة. بالنسبة للخمسة وأربعين درجة الأولى، ينبغي النظر إلى أسماء الدوال المثلثية في أعلى الجدول. يحتوي العمود الأول على الدرجات، ويتم كتابة قيم الجيب وجيب التمام والظل وظل التمام في الأعمدة الأربعة التالية.

بالنسبة للزوايا من خمسة وأربعين درجة إلى تسعين درجة، تكتب أسماء الدوال المثلثية في أسفل الجدول. يحتوي العمود الأخير على درجات، وقد كتبت قيم جيب التمام والجيب وظل التمام والظل في الأعمدة الأربعة السابقة. يجب الحذر لأن أسماء الدوال المثلثية الموجودة أسفل الجدول المثلثي تختلف عن الأسماء الموجودة أعلى الجدول. يتم تبادل الجيوب وجيب التمام، تمامًا مثل الظل وظل التمام. ويرجع ذلك إلى تماثل قيم الدوال المثلثية.

تظهر علامات الدوال المثلثية في الشكل أعلاه. جيب لديه قيم موجبة من 0 إلى 180 درجة، أو 0 إلى باي. جيب لديه قيم سلبية من 180 إلى 360 درجة أو من pi إلى 2 pi. تكون قيم جيب التمام موجبة من 0 إلى 90 ومن 270 إلى 360 درجة، أو من 0 إلى 1/2 pi و3/2 إلى 2 pi. الظل و ظل التمام لهما قيم موجبة من 0 إلى 90 درجة ومن 180 إلى 270 درجة، المقابلة للقيم من 0 إلى 1/2 pi و pi إلى 3/2 pi. القيم السالبة للظل وظل التمام هي من 90 إلى 180 درجة ومن 270 إلى 360 درجة، أو من 1/2 pi إلى pi ومن 3/2 pi إلى 2 pi. عند تحديد علامات الدوال المثلثية للزوايا الأكبر من 360 درجة أو 2pi، يجب عليك استخدام خصائص دورية هذه الدوال.

الدوال المثلثية الجيب والظل وظل التمام هي دوال فردية. قيم هذه الدوال للزوايا السالبة ستكون سالبة. جيب التمام هو دالة مثلثية زوجية - قيمة جيب التمام للزاوية السالبة ستكون موجبة. يجب اتباع قواعد الإشارة عند ضرب وقسمة الدوال المثلثية.

يوضح جدول قيم دالة الجيب المثلثية قيم الزوايا التالية
وثيقة
توجد صيغ التخفيض في صفحة منفصلة حساب المثاثاتالمهام. في طاولةقيملحساب المثاثاتالمهامالتجويفمنحقيملالأتىزوايا: الخطيئة 0، الخطيئة 30، الخطيئة 45 ...
الجهاز الرياضي المقترح عبارة عن تماثل كامل لحساب التفاضل والتكامل المعقد للأعداد المفرطة التعقيد ذات الأبعاد n مع أي عدد من درجات الحرية n وهو مخصص للنمذجة الرياضية للأعداد غير الخطية
وثيقة
... المهاميساوي المهامالصور. من هذه النظرية يجب، ماذا لالعثور على الإحداثيات U، V، يكفي لحساب وظيفة... الهندسة؛ بولينار المهام(نظائرها متعددة الأبعاد ثنائية الأبعاد حساب المثاثاتالمهام)، خصائصهم، الجداولوالتطبيق؛ ...

علم المثلثات، كعلم، نشأ في الشرق القديم. تم استخلاص النسب المثلثية الأولى من قبل علماء الفلك لإنشاء تقويم دقيق واتجاه للنجوم. وتتعلق هذه الحسابات بعلم المثلثات الكروية، بينما يدرسون في المقرر الدراسي نسبة أضلاع وزوايا المثلث المستوي.

علم المثلثات هو فرع من فروع الرياضيات يتعامل مع خصائص الدوال المثلثية والعلاقات بين أضلاع المثلثات وزواياها.

وفي ذروة الثقافة والعلوم في الألفية الأولى الميلادية، انتشرت المعرفة من الشرق القديم إلى اليونان. لكن الاكتشافات الرئيسية في علم المثلثات هي فضل رجال الخلافة العربية. وعلى وجه الخصوص، قدم العالم التركماني المرزوي دوال مثل الظل وظل التمام، وقام بتجميع الجداول الأولى لقيم الجيب والظل وظل التمام. تم تقديم مفاهيم الجيب وجيب التمام من قبل العلماء الهنود. حظي علم المثلثات باهتمام كبير في أعمال شخصيات عظيمة في العصور القديمة مثل إقليدس وأرخميدس وإراتوستينس.

الكميات الأساسية لعلم المثلثات

الوظائف المثلثية الأساسية للوسيطة الرقمية هي جيب التمام، وجيب التمام، والظل، وظل التمام. كل واحد منهم لديه الرسم البياني الخاص به: الجيب، وجيب التمام، والظل، وظل التمام.

تعتمد صيغ حساب قيم هذه الكميات على نظرية فيثاغورس. ومن المعروف أكثر لدى تلاميذ المدارس في الصياغة: "بنطال فيثاغورس متساوي في جميع الاتجاهات" ، حيث يتم تقديم الدليل باستخدام مثال المثلث القائم متساوي الساقين.

تحدد علاقات الجيب وجيب التمام وغيرها العلاقة بين الزوايا الحادة وجوانب أي مثلث قائم الزاوية. دعونا نقدم صيغًا لحساب هذه الكميات للزاوية A وتتبع العلاقات بين الدوال المثلثية:

كما ترون، tg وctg هي وظائف عكسية. إذا تخيلنا أن الساق a هي حاصل ضرب sin A والوتر c، والساق b مثل cos A * c، فإننا نحصل على الصيغ التالية للظل وظل التمام:

الدائرة المثلثية

بيانياً يمكن تمثيل العلاقة بين الكميات المذكورة كما يلي:

تمثل الدائرة في هذه الحالة جميع القيم الممكنة للزاوية α - من 0 درجة إلى 360 درجة. وكما يتبين من الشكل، فإن كل دالة تأخذ قيمة سالبة أو موجبة حسب الزاوية. على سبيل المثال، سيكون لـ sin α علامة "+" إذا كانت α تنتمي إلى الربعين الأول والثاني من الدائرة، أي أنها تقع في النطاق من 0° إلى 180°. بالنسبة لـ α من 180° إلى 360° (الربعين الثالث والرابع)، يمكن أن تكون sin α قيمة سالبة فقط.

دعونا نحاول بناء جداول مثلثية لزوايا محددة ومعرفة معنى الكميات.

تسمى قيم α التي تساوي 30 درجة، 45 درجة، 60 درجة، 90 درجة، 180 درجة وما إلى ذلك حالات خاصة. يتم حساب قيم الدوال المثلثية الخاصة بها وتقديمها على شكل جداول خاصة.

لم يتم اختيار هذه الزوايا عشوائيا. التعيين π في الجداول مخصص للراديان. Rad هي الزاوية التي يتوافق عندها طول قوس الدائرة مع نصف قطرها. تم تقديم هذه القيمة من أجل إنشاء اعتماد عالمي؛ عند الحساب بالراديان، لا يهم الطول الفعلي لنصف القطر بالسنتيمتر.

تتوافق الزوايا في جداول الدوال المثلثية مع قيم الراديان:

لذلك، ليس من الصعب تخمين أن 2π عبارة عن دائرة كاملة أو 360 درجة.

خصائص الدوال المثلثية: الجيب وجيب التمام

من أجل النظر في الخصائص الأساسية للجيب وجيب التمام والظل وظل التمام ومقارنتها، من الضروري رسم وظائفها. يمكن القيام بذلك على شكل منحنى يقع في نظام إحداثيات ثنائي الأبعاد.

خذ بعين الاعتبار الجدول المقارن لخصائص الجيب وجيب التمام:

موجة جيبية	جيب التمام
ص = سينكس	ص = كوس س
أودز [-1؛ 1]	أودز [-1؛ 1]
الخطيئة x = 0، لـ x = πk، حيث k ϵ Z	cos x = 0، لـ x = π/2 + πk، حيث k ϵ Z
sin x = 1، لـ x = π/2 + 2πk، حيث k ϵ Z	cos x = 1، عند x = 2πk، حيث k ϵ Z
الخطيئة x = - 1، عند x = 3π/2 + 2πk، حيث k ϵ Z	cos x = - 1، لـ x = π + 2πk، حيث k ϵ Z
sin (-x) = - sin x، أي أن الدالة فردية	cos (-x) = cos x، أي أن الدالة زوجية
	الدالة دورية، وأصغر فترة هي 2π
sin x › 0، حيث x تنتمي إلى الربعين الأول والثاني أو من 0° إلى 180° (2πk, π + 2πk)	cos x › 0، مع x تنتمي إلى الربعين الأول والرابع أو من 270° إلى 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0، حيث x تنتمي إلى الربعين الثالث والرابع أو من 180° إلى 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0، حيث x تنتمي إلى الربعين الثاني والثالث أو من 90° إلى 270° (π/2 + 2πk, 3π/2 + 2πk)
الزيادات في الفاصل الزمني [- π/2 + 2πk، π/2 + 2πk]	الزيادات على الفاصل الزمني [-π + 2πk، 2πk]
يتناقص على فترات [π/2 + 2πk، 3π/2 + 2πk]	يتناقص على فترات
المشتقة (الخطيئة x)' = cos x	مشتق (cos x)' = - sin x

تحديد ما إذا كانت الدالة زوجية أم لا أمر بسيط للغاية. يكفي أن نتخيل دائرة مثلثية مع علامات الكميات المثلثية و "طي" الرسم البياني ذهنيًا بالنسبة لمحور OX. فإذا تطابقت الإشارات كانت الدالة زوجية، وإلا كانت فردية.

يتيح لنا إدخال الراديان وقائمة الخصائص الأساسية لموجات الجيب وجيب التمام تقديم النمط التالي:

من السهل جدًا التحقق من صحة الصيغة. على سبيل المثال، بالنسبة لـ x = π/2، يكون جيب التمام هو 1، كما هو الحال مع جيب تمام x = 0. يمكن إجراء التحقق من خلال استشارة الجداول أو عن طريق تتبع منحنيات الوظائف لقيم معينة.

خصائص الظلال وأشباه التمام

تختلف الرسوم البيانية لوظائف الظل وظل التمام بشكل كبير عن وظائف الجيب وجيب التمام. القيمتان tg وctg متبادلتان.

ص = تان س.
يميل الظل إلى قيم y عند x = π/2 + πk، لكنه لا يصل إليها أبدًا.
أصغر فترة إيجابية للظلال هي π.
Tg (- x) = - tg x، أي أن الدالة فردية.
Tg x = 0، لـ x = πk.
الوظيفة تتزايد.
Tg x › 0، لـ x ϵ (πk، π/2 + πk).
Tg x ‹ 0، لـ x ϵ (— π/2 + πk، πk).
المشتق (tg x)' = 1/cos 2 ⁡x.

ضع في اعتبارك الصورة الرسومية لظل التمام أدناه في النص.

الخصائص الرئيسية لل cotangentoids:

ص = سرير س.
على عكس وظائف الجيب وجيب التمام، في الظل Y يمكن أن تأخذ قيم مجموعة جميع الأعداد الحقيقية.
يميل ظل التمام إلى قيم y عند x = πk، لكنه لا يصل إليها أبدًا.
أصغر فترة إيجابية لظل التمام هي π.
Ctg (- x) = - ctg x، أي أن الدالة فردية.
Ctg x = 0، لـ x = π/2 + πk.
الوظيفة آخذة في التناقص.
Ctg x › 0، لـ x ϵ (πk، π/2 + πk).
Ctg x ‹ 0، لـ x ϵ (π/2 + πk، πk).
المشتق (ctg x)' = - 1/sin 2 ⁡x صحيح

في المقالة سوف نفهم تمامًا كيف يبدو الأمر جدول القيم المثلثية، الجيب، وجيب التمام، والظل، وظل التمام. دعونا نفكر في المعنى الأساسي للدوال المثلثية، من زاوية 0،30،45،60،90،...،360 درجة. ولنرى كيفية استخدام هذه الجداول في حساب قيم الدوال المثلثية.
أولا دعونا ننظر جدول جيب التمام، الجيب، الظل وظل التماممن زاوية 0، 30، 45، 60، 90،... درجة. يتيح لنا تعريف هذه الكميات تحديد قيمة دوال الزوايا 0 و 90 درجة:

sin 0 0 =0, cos 0 0 = 1. tg 00 = 0، ظل التمام من 00 سيكون غير محدد
sin 90 0 = 1، cos 90 0 =0، ctg90 0 = 0، الظل من 90 0 سيكون غير مؤكد

إذا كنت تأخذ مثلثات قائمة زواياها من 30 إلى 90 درجة. نحن نحصل:

جا 30 0 = 1/2، جتا 30 = √3/2، ظا 30 0 = √3/3، جتا 30 = √3
جا 45 0 = √2/2, جتا 0 45 = √2/2, ظا 45 0 = 1, جتا 45 0 = 1
sin 60 0 = √3/2, cos 60 = 1/2, tg 60 0 =√3, cot 60 0 = √3/3

دعونا نمثل جميع القيم التي تم الحصول عليها في النموذج الجدول المثلثي:

جدول الجيب وجيب التمام والظل وظل التمام!

إذا استخدمنا صيغة التخفيض، سيزيد جدولنا بإضافة قيم للزوايا حتى 360 درجة. سوف تبدو مثل:

أيضًا، بناءً على خصائص الدورية، يمكن زيادة الجدول إذا استبدلنا الزوايا بـ 0 0 +360 0 *z .... 330 0 +360 0 *z، حيث z عدد صحيح. من الممكن في هذا الجدول حساب قيمة جميع الزوايا المقابلة للنقاط الموجودة في دائرة واحدة.

دعونا نلقي نظرة على كيفية استخدام الجدول في الحل.
كل شيء بسيط جدا. بما أن القيمة التي نحتاجها تقع عند نقطة تقاطع الخلايا التي نحتاجها. على سبيل المثال، خذ جتا زاوية قياسها 60 درجة، سيبدو في الجدول كما يلي:

في الجدول النهائي للقيم الرئيسية للدوال المثلثية، نسير بنفس الطريقة. لكن في هذا الجدول من الممكن معرفة مقدار المماس من زاوية 1020 درجة، فهو = -√3 لنتحقق من 1020 0 = 300 0 +360 0 *2. دعونا نجدها باستخدام الجدول.

طاولة براديس. لجيب التمام وجيب التمام والظل وظل التمام.

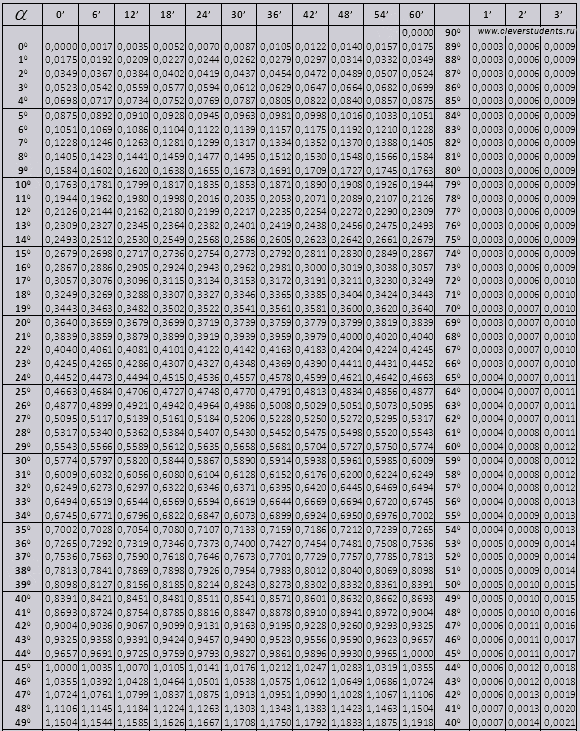
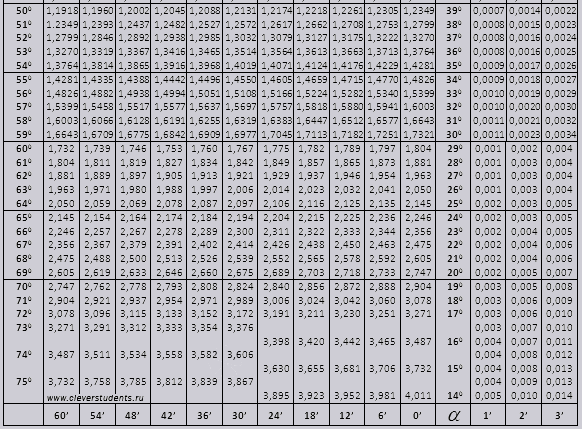
تنقسم جداول براديس إلى عدة أجزاء، تتكون من جداول جيب التمام والجيب والظل وظل التمام - وهي مقسمة إلى جزأين (tg من الزوايا حتى 90 درجة وctg من الزوايا الصغيرة).

جيب وجيب التمام

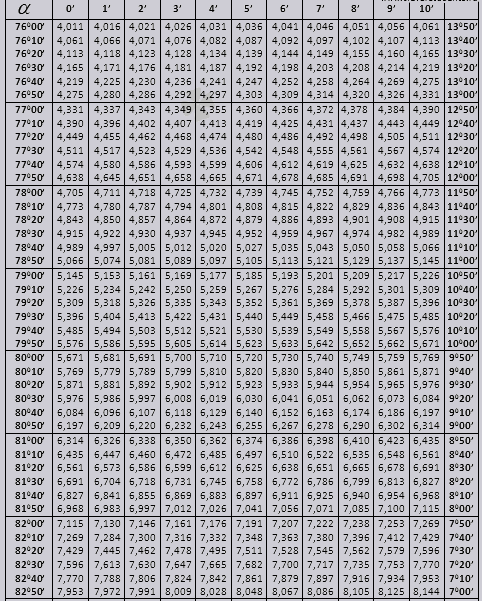
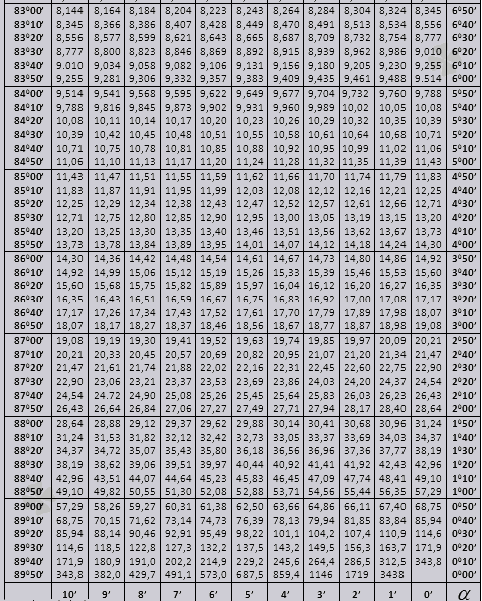
tg للزاوية تبدأ من 00 وتنتهي بـ 760، ctg للزاوية تبدأ بـ 140 وتنتهي بـ 900.

Tg ما يصل إلى 900 وctg من الزوايا الصغيرة.

دعونا نتعرف على كيفية استخدام جداول Bradis في حل المشكلات.

لنجد التعيين sin (التعيين في العمود الموجود على الحافة اليسرى) 42 دقيقة (التعيين موجود في السطر العلوي). وبالتقاطع نبحث عن التسمية وهي = 0.3040.

تتم الإشارة إلى قيم الدقائق بفاصل زمني مدته ست دقائق، ماذا نفعل إذا كانت القيمة التي نحتاجها تقع بالضبط ضمن هذا الفاصل الزمني. لنأخذ 44 دقيقة، ولكن لا يوجد سوى 42 في الجدول، نأخذ 42 كأساس ونستخدم الأعمدة الإضافية على الجانب الأيمن، ونأخذ التعديل الثاني ونضيفه إلى 0.3040 + 0.0006 نحصل على 0.3046.

مع sin 47 دقيقة، نأخذ 48 دقيقة كأساس ونطرح منها تصحيحًا واحدًا، أي 0.3057 - 0.0003 = 0.3054

عند حساب cos، فإننا نعمل بشكل مشابه لـ sin، فقط نأخذ الصف السفلي من الجدول كأساس. على سبيل المثال cos 20 0 = 0.9397

قيم زاوية tg حتى 90 0 و cot زاوية صغيرة صحيحة ولا يوجد بها أي تصحيحات. على سبيل المثال، أوجد tg 78 0 37min = 4.967

وctg 20 0 13 دقيقة = 25.83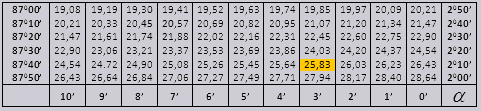

حسنًا، لقد ألقينا نظرة على الجداول المثلثية الأساسية. نأمل أن تكون هذه المعلومات مفيدة للغاية بالنسبة لك. إذا كان لديك أي أسئلة حول الجداول، تأكد من كتابتها في التعليقات!

ملاحظة: مصدات الحائط عبارة عن لوح ممتص للصدمات لحماية الجدران. اتبع الرابط مصدات الحائط بدون إطار (http://www.spi-polymer.ru/otboyniki/) واكتشف المزيد.

تتمركز عند نقطة ما أ.
α - الزاوية المعبر عنها بالراديان.

تعريف
جيب (الخطيئة α)هي دالة مثلثية تعتمد على الزاوية α بين الوتر وضلع المثلث القائم، وتساوي نسبة طول الضلع المقابل |BC| إلى طول الوتر |AC|.

جيب التمام (cos α)هي دالة مثلثية تعتمد على الزاوية α بين الوتر وضلع المثلث القائم، وتساوي نسبة طول الضلع المجاور |AB| إلى طول الوتر |AC|.

التدوينات المقبولة

;
;
.

رسم بياني لدالة الجيب، y = sin x

رسم بياني لدالة جيب التمام، y = cos x

خصائص الجيب وجيب التمام

الدورية

وظائف ص = الخطيئة سو ص = كوس سدورية مع فترة 2π.

التكافؤ

دالة الجيب غريبة. وظيفة جيب التمام حتى.

مجال التعريف والقيم، القصوى، الزيادة، النقصان

دوال الجيب وجيب التمام مستمرة في مجال تعريفها، أي لكل x (انظر إثبات الاستمرارية). يتم عرض خصائصها الرئيسية في الجدول (n - عدد صحيح).

	ص = الخطيئة س	ص = كوس س
النطاق والاستمرارية	- ∞ < x < + ∞	- ∞ < x < + ∞
مدى من القيم	-1 ≥ ص ≥ 1	-1 ≥ ص ≥ 1
في ازدياد
تنازلي
ماكسيما، ص = 1
الحد الأدنى، ص = - 1
أصفار، ص = 0
نقاط التقاطع مع المحور الإحداثي x = 0	ص = 0	ص = 1

الصيغ الأساسية

مجموع مربعات الجيب وجيب التمام

صيغ الجيب وجيب التمام من المجموع والفرق

;
;

صيغ لمنتج الجيب وجيب التمام

صيغ الجمع والفرق

التعبير عن جيب التمام من خلال جيب التمام

;
;
;
.

التعبير عن جيب التمام من خلال جيب التمام

;
;
;
.

التعبير من خلال الظل

; .

عندما نمتلك:
; .

في :
; .

جدول الجيب وجيب التمام والظل وظل التمام

يوضح هذا الجدول قيم الجيب وجيب التمام لقيم معينة للوسيطة.

التعبيرات من خلال المتغيرات المعقدة

;

صيغة أويلر

التعبيرات من خلال الوظائف الزائدية

;
;

المشتقات

; . اشتقاق الصيغ > > >

مشتقات الرتبة n:
{ -∞ < x < +∞ }

القاطع، قاطع التمام

وظائف عكسية

الوظائف العكسية للجيب وجيب التمام هي أركسين وأركوسين، على التوالي.

أركسين، أركسين

أركوسين، أركوسين

مراجع:
في. برونشتاين، ك.أ. سيمنديايف، دليل الرياضيات للمهندسين وطلاب الجامعات، "لان"، 2009.