Bradis cədvəlinə görə kosinus 30. Sinus (sin x) və kosinus (cos x) – xassələr, qrafiklər, düsturlar

0, 30, 45, 60, 90, ... dərəcə bucaqları üçün əsas triqonometrik funksiyalar cədvəli

$\sin$, $\cos$, $\tan$ və $\cot$ funksiyalarının triqonometrik təriflərindən $0$ və $90$ dərəcə bucaqları üçün onların dəyərlərini öyrənə bilərsiniz:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ müəyyən edilməyib;

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ müəyyən edilmir.

Məktəb həndəsə kursunda düz üçbucaqları öyrənərkən $0°$, $30°$, $45°$, $60°$ və $90°$ bucaqlarının triqonometrik funksiyaları tapılır.

Göstərilən bucaqlar üçün müvafiq olaraq dərəcə və radyanlarda triqonometrik funksiyaların qiymətləri tapıldı ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\) pi)(3) $, $\frac(\pi)(2)$) yadda saxlamaq və istifadə etmək asanlığı üçün adlı cədvələ daxil edilir. triqonometrik cədvəl, triqonometrik funksiyaların əsas dəyərlərinin cədvəli və s.

Azaltma düsturlarından istifadə edərkən triqonometrik cədvəl $360°$ və müvafiq olaraq $2\pi$ radian bucağı ilə genişləndirilə bilər:

Triqonometrik funksiyaların dövrilik xüsusiyyətlərindən istifadə edərək, artıq məlum olandan $360°$ ilə fərqlənəcək hər bir bucaq hesablana və cədvəldə qeyd edilə bilər. Məsələn, $0°$ bucaq üçün triqonometrik funksiya $0°+360°$ bucaq və $0°+2 \cdot 360°$ və $0°+3 \cdot 360°$ bucaq üçün eyni dəyərə malik olacaq. və s.

Triqonometrik cədvəldən istifadə edərək vahid dairənin bütün bucaqlarının dəyərlərini təyin edə bilərsiniz.

Məktəb həndəsə kursunda triqonometrik məsələlərin həllinin rahatlığı üçün triqonometrik cədvəldə toplanmış triqonometrik funksiyaların əsas dəyərlərini yadda saxlamalısan.

Cədvəldən istifadə

Cədvəldə tələb olunan triqonometrik funksiyanı və bu funksiyanın hesablanması lazım olan bucağın və ya radanın qiymətini tapmaq kifayətdir. Funksiya ilə sətrin və qiymətli sütunun kəsişməsində verilmiş arqumentin triqonometrik funksiyasının istənilən qiymətini alırıq.

Şəkildə siz $\frac(1)(2)$-a bərabər olan $\cos⁡60°$ dəyərinin necə tapılacağını görə bilərsiniz.

Genişləndirilmiş triqonometrik cədvəl eyni şəkildə istifadə olunur. Onun istifadəsinin üstünlüyü, artıq qeyd edildiyi kimi, demək olar ki, istənilən bucağın triqonometrik funksiyasının hesablanmasıdır. Məsələn, siz asanlıqla $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 dəyərini tapa bilərsiniz. °$:

Əsas triqonometrik funksiyaların Bradis cədvəlləri

Dərəcələrin tam dəyəri və dəqiqələrin tam dəyəri üçün tamamilə istənilən bucaq dəyərinin triqonometrik funksiyasını hesablamaq imkanı Bradis cədvəllərinin istifadəsi ilə təmin edilir. Məsələn, $\cos⁡34°7"$ dəyərini tapın. Cədvəllər 2 hissəyə bölünür: $\sin$ və $\cos$ dəyərlərinin cədvəli və $ dəyərlərinin cədvəli \tan$ və $\cot$.

Bradis cədvəlləri triqonometrik funksiyaların təxmini dəyərlərini 4 onluq yerə qədər dəqiqliklə əldə etməyə imkan verir.

Bradis masalarından istifadə

Sinuslar üçün Bradis cədvəllərindən istifadə edərək $\sin⁡17°42"$ tapırıq. Bunun üçün sinuslar və kosinuslar cədvəlinin sol sütununda dərəcələrin qiymətini tapırıq - $17°$ və yuxarı sətirdə dəqiqələrin dəyərini tapırıq - $42"$. Onların kəsişməsində istənilən dəyəri əldə edirik:

$\sin17°42"=0,304$.

$\sin17°44"$ dəyərini tapmaq üçün cədvəlin sağ tərəfindəki düzəlişdən istifadə etməlisiniz. Bu halda cədvəldə olan $42"$ dəyərinə $2 üçün düzəliş əlavə etməlisiniz. "$, $0,0006$-a bərabərdir. Alırıq:

$\sin17°44"=0,304+0,0006=0,3046$.

$\sin17°47"$ dəyərini tapmaq üçün cədvəlin sağ tərəfindəki düzəlişdən də istifadə edirik, yalnız bu halda $\sin17°48"$ qiymətini əsas götürürük və $1"$ üçün düzəlişi çıxarırıq. :

$\sin17°47"=0,3057-0,0003=0,3054$.

Kosinusları hesablayarkən oxşar hərəkətləri yerinə yetiririk, lakin biz sağ sütunda dərəcələrə, cədvəlin alt sütununda isə dəqiqələrə baxırıq. Məsələn, $\cos20°=0,9397$.

$90°$-a qədər olan tangens dəyərləri və kiçik bucaq kotangensi üçün heç bir düzəliş yoxdur. Məsələn, cədvələ görə $4.967$-a bərabər olan $\tan 78°37"$ tapaq.

TRIQONOMETRİK FUNKSİYALARIN QİYMƏTLƏR CƏDVƏLİ

Triqonometrik funksiyaların qiymətləri cədvəli 0, 30, 45, 60, 90, 180, 270 və 360 dərəcə bucaqlar və vradianlarda müvafiq bucaq qiymətləri üçün tərtib edilmişdir. Cədvəldə triqonometrik funksiyalardan sinus, kosinus, tangens, kotangens, sekant və kosekant göstərilir. Məktəb nümunələrinin həllinin rahatlığı üçün cədvəldəki triqonometrik funksiyaların dəyərləri ədədlərin kvadrat kökünü çıxarmaq üçün işarələri qoruyarkən kəsr şəklində yazılır ki, bu da çox vaxt mürəkkəb riyazi ifadələri azaltmağa kömək edir. Tangens və kotangens üçün bəzi bucaqların dəyərləri müəyyən edilə bilməz. Belə bucaqların tangens və kotangens dəyərləri üçün triqonometrik funksiyaların qiymətləri cədvəlində tire var. Belə bucaqların tangensi və kotangensi sonsuzluğa bərabərdir ki, ümumiyyətlə qəbul edilir. Ayrı bir səhifədə triqonometrik funksiyaları azaltmaq üçün düsturlar var.

Triqonometrik sinus funksiyası üçün dəyərlər cədvəli aşağıdakı bucaqlar üçün dəyərləri göstərir: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360, bu da uyğun gəlir. sin 0 pi, sin pi/6 , sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi bucaqların radian ölçüsündə. Sinusların məktəb cədvəli.

Triqonometrik kosinus funksiyası üçün cədvəldə aşağıdakı bucaqlar üçün dəyərlər göstərilir: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360, bu da cos 0 pi-yə uyğundur. , bucaqların radian ölçüsündə cos pi 6, cos pi 4, cos pi 3, cos pi 2, cos pi, cos 3 pi 2, cos 2 pi. Məktəb kosinus cədvəli.

Triqonometrik tangens funksiyası üçün triqonometrik cədvəl aşağıdakı bucaqlar üçün dəyərlər verir: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360, bu da tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi bucaqların radian ölçüsündə. Triqonometrik tangens funksiyalarının aşağıdakı qiymətləri tan 90, tan 270, tan pi/2, tan 3 pi/2 təyin edilmir və sonsuzluğa bərabər hesab olunur.

Triqonometrik cədvəldə triqonometrik funksiya kotangenti üçün aşağıdakı bucaqların qiymətləri verilmişdir: dərəcə ölçüsündə ctg 30, ctg 45, ctg 60, ctg 90, ctg 270, bu da ctg pi/6, ctg pi/4-ə uyğundur. , ctg pi/3, tg pi/ 2, tan 3 pi/2 bucaqların radian ölçüsündə. Triqonometrik kotangent funksiyaların aşağıdakı qiymətləri ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi kimi müəyyən edilmir və sonsuzluğa bərabər hesab olunur.

Sekant və kosekant triqonometrik funksiyalarının qiymətləri sinus, kosinus, tangens, kotangens kimi dərəcə və radyanlarda eyni bucaqlar üçün verilir.

Qeyri-standart bucaqların triqonometrik funksiyalarının qiymətləri cədvəli 15, 18, 22.5, 36, 54, 67.5 72 dərəcə və radian pi/12 bucaqlar üçün sinus, kosinus, tangens və kotangens dəyərlərini göstərir. , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 radyan. Məktəb nümunələrində kəsrləri azaltmağı asanlaşdırmaq üçün triqonometrik funksiyaların dəyərləri kəsrlər və kvadrat köklərlə ifadə edilir.

Daha üç triqonometriya canavarı. Birincisi, 1,5 bir yarım dərəcə və ya pi-nin 120-yə bölünən tangensidir. İkincisi, pi-nin 240-a bölünən kosinusu, pi/240. Ən uzunu, pi kosinusu 17-yə bölünür, pi/17.

Sinus və kosinus funksiyalarının dəyərlərinin triqonometrik dairəsi bucağın böyüklüyündən asılı olaraq sinus və kosinusun əlamətlərini vizual olaraq təmsil edir. Xüsusilə sarışınlar üçün, qarışıqlığı azaltmaq üçün kosinus dəyərləri yaşıl tire ilə vurğulanır. Radianlar pi ilə ifadə edildikdə dərəcələrin radana çevrilməsi də çox aydın şəkildə təqdim olunur.

Bu triqonometrik cədvəl bir dərəcə intervalla 0 sıfırdan 90 doxsan dərəcəyə qədər olan bucaqlar üçün sinus, kosinus, tangens və kotangens dəyərlərini təqdim edir. İlk qırx beş dərəcə üçün triqonometrik funksiyaların adlarına cədvəlin yuxarı hissəsində baxmaq lazımdır. Birinci sütunda dərəcələr var, sinusların, kosinusların, tangenslərin və kotangentlərin dəyərləri sonrakı dörd sütunda yazılır.

Qırx beş dərəcədən doxsan dərəcəyə qədər olan bucaqlar üçün triqonometrik funksiyaların adları cədvəlin aşağı hissəsində yazılır. Sonuncu sütun dərəcələri ehtiva edir; kosinusların, sinusların, kotangentlərin və tangenslərin dəyərləri əvvəlki dörd sütunda yazılır. Diqqətli olmalısınız, çünki triqonometrik cədvəlin altındakı triqonometrik funksiyaların adları cədvəlin yuxarısındakı adlardan fərqlidir. Tangens və kotangens kimi sinuslar və kosinuslar bir-birini əvəz edir. Bu, triqonometrik funksiyaların qiymətlərinin simmetriyası ilə əlaqədardır.

Triqonometrik funksiyaların əlamətləri yuxarıdakı şəkildə göstərilmişdir. Sinus 0-dan 180 dərəcəyə qədər və ya 0-dan pi-yə qədər müsbət dəyərlərə malikdir. Sine 180-dən 360 dərəcəyə qədər və ya pi-dən 2 pi-yə qədər mənfi dəyərlərə malikdir. Kosinus dəyərləri 0 ilə 90 və 270 ilə 360 dərəcə arasında müsbətdir və ya 0 ilə 1/2 pi və 3/2 ilə 2 pi arasındadır. Tangens və kotangens 0 ilə 90 dərəcə arasında və 180 ilə 270 dərəcə arasında müsbət dəyərlərə malikdir, 0-dan 1/2 pi və pi-dən 3/2 pi-ə qədər olan dəyərlərə uyğundur. Tangens və kotangensin mənfi dəyərləri 90 ilə 180 dərəcə və 270 ilə 360 dərəcə arasında və ya 1/2 pi ilə pi və 3/2 pi ilə 2 pi arasındadır. 360 dərəcədən və ya 2 pi-dən çox bucaqlar üçün triqonometrik funksiyaların əlamətlərini təyin edərkən bu funksiyaların dövrilik xassələrindən istifadə etməlisiniz.

Triqonometrik funksiyalar sinus, tangens və kotangens tək funksiyalardır. Mənfi bucaqlar üçün bu funksiyaların dəyərləri mənfi olacaq. Kosinus bərabər triqonometrik funksiyadır - mənfi bucaq üçün kosinus dəyəri müsbət olacaqdır. Triqonometrik funksiyaların vurulması və bölünməsi zamanı işarə qaydalarına əməl edilməlidir.

Triqonometrik sinus funksiyası üçün dəyərlər cədvəli aşağıdakı açılar üçün dəyərləri göstərir
Sənəd
Ayrı bir səhifədə azalma düsturları var triqonometrikfunksiyaları. IN masadəyərlərüçüntriqonometrikfunksiyalarısinusverilmişdirdəyərlərüçünnövbətikünclər: günah 0, günah 30, günah 45 ...
Təklif olunan riyazi aparat istənilən sayda sərbəstlik dərəcəsi n olan n ölçülü hiperkompleks ədədlər üçün kompleks hesablamanın tam analoqudur və qeyri-xətti riyazi modelləşdirmə üçün nəzərdə tutulub.
Sənəd
... funksiyaları bərabərdir funksiyalarıŞəkillər. Bu teoremdən etməlidir, Nə üçün U, V koordinatlarını tapmaq, hesablamaq kifayətdir funksiyası... həndəsə; polinar funksiyaları(iki ölçülü çoxölçülü analoqları triqonometrikfunksiyaları), onların xüsusiyyətləri, masalar və tətbiqi; ...

Triqonometriya bir elm olaraq Qədim Şərqdə yaranmışdır. İlk triqonometrik nisbətlər ulduzlar tərəfindən dəqiq təqvim və oriyentasiya yaratmaq üçün astronomlar tərəfindən əldə edilmişdir. Bu hesablamalar sferik triqonometriya ilə əlaqədardır, məktəb kursunda isə müstəvi üçbucağın tərəflərinin və bucaqlarının nisbətini öyrənirlər.

Triqonometriya triqonometrik funksiyaların xassələri və üçbucaqların tərəfləri və bucaqları arasındakı əlaqə ilə məşğul olan riyaziyyatın bir sahəsidir.

Eramızın 1-ci minilliyində mədəniyyət və elmin çiçəkləndiyi dövrdə bilik Qədim Şərqdən Yunanıstana yayıldı. Lakin triqonometriyanın əsas kəşfləri Ərəb xilafətinin kişilərinin xidmətləridir. Xüsusilə, türkmən alimi əl-Mərəzvi tangens və kotangens kimi funksiyaları təqdim etmiş, sinuslar, tangenslər və kotangenslər üçün ilk qiymət cədvəllərini tərtib etmişdir. Sinus və kosinus anlayışları hind alimləri tərəfindən təqdim edilmişdir. Evklid, Arximed və Eratosfen kimi antik dövrün dahi şəxsiyyətlərinin əsərlərində triqonometriyaya böyük diqqət yetirilmişdir.

Triqonometriyanın əsas kəmiyyətləri

Rəqəmsal arqumentin əsas triqonometrik funksiyaları sinus, kosinus, tangens və kotangensdir. Onların hər birinin öz qrafiki var: sinus, kosinus, tangens və kotangens.

Bu kəmiyyətlərin dəyərlərini hesablamaq üçün düsturlar Pifaqor teoreminə əsaslanır. Məktəblilərə daha yaxşı məlumdur: "Bütün istiqamətlərdə bərabər Pifaqor şalvarları", çünki sübut ikitərəfli düzbucaqlı üçbucaq nümunəsi ilə verilir.

Sinus, kosinus və digər əlaqələr istənilən düzbucaqlı üçbucağın iti bucaqları və tərəfləri arasında əlaqə yaradır. Gəlin A bucağı üçün bu kəmiyyətləri hesablamaq üçün düsturları təqdim edək və triqonometrik funksiyalar arasındakı əlaqələri izləyək:

Gördüyünüz kimi tg və ctg tərs funksiyalardır. Əgər a ayağını sin A və hipotenuzanın c məhsulu, b ayağını isə cos A * c kimi təsəvvür etsək, tangens və kotangens üçün aşağıdakı düsturları alırıq:

Triqonometrik dairə

Qrafik olaraq qeyd olunan kəmiyyətlər arasındakı əlaqə aşağıdakı kimi göstərilə bilər:

Dairə, bu halda, α bucağının bütün mümkün dəyərlərini təmsil edir - 0 ° ilə 360 ° arasında. Şəkildən göründüyü kimi, hər bir funksiya bucaqdan asılı olaraq mənfi və ya müsbət qiymət alır. Məsələn, α dairənin 1-ci və 2-ci rübünə aiddirsə, yəni 0°-dən 180°-ə qədər diapazonda olarsa, sin α “+” işarəsinə malik olacaqdır. 180°-dən 360°-yə qədər (III və IV rüblər) α üçün sin α yalnız mənfi qiymət ola bilər.

Gəlin konkret açılar üçün triqonometrik cədvəllər qurmağa və kəmiyyətlərin mənasını öyrənməyə çalışaq.

30°, 45°, 60°, 90°, 180° və s.-ə bərabər olan α qiymətləri xüsusi hallar adlanır. Onlar üçün triqonometrik funksiyaların dəyərləri hesablanır və xüsusi cədvəllər şəklində təqdim olunur.

Bu açılar təsadüfi seçilməmişdir. Cədvəllərdə π təyinatı radyanlar üçündür. Rad dairənin qövsünün uzunluğunun onun radiusuna uyğun olduğu bucaqdır. Bu dəyər universal bir asılılıq yaratmaq üçün tətbiq edilmişdir; radyanla hesablayarkən, radiusun sm ilə həqiqi uzunluğunun əhəmiyyəti yoxdur.

Triqonometrik funksiyalar üçün cədvəllərdəki bucaqlar radian qiymətlərinə uyğundur:

Beləliklə, 2π-nin tam çevrə və ya 360° olduğunu təxmin etmək çətin deyil.

Triqonometrik funksiyaların xassələri: sinus və kosinus

Sinus və kosinusun, tangens və kotangensin əsas xassələrini nəzərdən keçirmək və müqayisə etmək üçün onların funksiyalarını çəkmək lazımdır. Bu, iki ölçülü koordinat sistemində yerləşən əyri şəklində edilə bilər.

Sinus və kosinus üçün xassələrin müqayisəli cədvəlini nəzərdən keçirin:

Sinus dalğası	Kosinus
y = sinx	y = cos x
ODZ [-1; 1]	ODZ [-1; 1]
sin x = 0, x = πk üçün, burada k ϵ Z	cos x = 0, x = π/2 + πk üçün, burada k ϵ Z
sin x = 1, x = π/2 + 2πk üçün, burada k ϵ Z	cos x = 1, x = 2πk nöqtəsində, burada k ϵ Z
sin x = - 1, at x = 3π/2 + 2πk, burada k ϵ Z	cos x = - 1, x = π + 2πk üçün, burada k ϵ Z
sin (-x) = - sin x, yəni funksiya təkdir	cos (-x) = cos x, yəni funksiya cütdür
	funksiya dövri, ən kiçik dövr 2π-dir
sin x › 0, x 1-ci və 2-ci rüblərə aiddir və ya 0°-dən 180°-yə qədər (2πk, π + 2πk)	cos x › 0, x I və IV rüblərə aiddir və ya 270°-dən 90°-ə qədər (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, x üçüncü və dördüncü rüblərə aiddir və ya 180°-dən 360°-yə qədər (π + 2πk, 2π + 2πk)	cos x ‹ 0, x 2-ci və 3-cü rüblərə aiddir və ya 90°-dən 270°-yə qədər (π/2 + 2πk, 3π/2 + 2πk)
intervalında artır [- π/2 + 2πk, π/2 + 2πk]	[-π + 2πk, 2πk] intervalında artır
fasilələrlə azalır [π/2 + 2πk, 3π/2 + 2πk]	fasilələrlə azalır
törəmə (sin x)’ = cos x	törəmə (cos x)’ = - sin x

Bir funksiyanın cüt olub olmadığını müəyyən etmək çox sadədir. Triqonometrik kəmiyyətlərin əlamətləri olan bir triqonometrik dairəni təsəvvür etmək və OX oxuna nisbətən qrafiki zehni olaraq "qatlamaq" kifayətdir. İşarələr üst-üstə düşürsə, funksiya cüt, əks halda təkdir.

Radianların tətbiqi və sinus və kosinus dalğalarının əsas xüsusiyyətlərinin siyahısı bizə aşağıdakı nümunəni təqdim etməyə imkan verir:

Düsturun düzgünlüyünü yoxlamaq çox asandır. Məsələn, x = π/2 üçün sinus, x = 0-ın kosinusu kimi 1-dir. Yoxlama cədvəllərə müraciət etməklə və ya verilmiş qiymətlər üçün funksiya əyrilərini izləməklə edilə bilər.

Tangensoidlərin və kotangensoidlərin xassələri

Tangens və kotangens funksiyalarının qrafikləri sinus və kosinus funksiyalarından əhəmiyyətli dərəcədə fərqlənir. tg və ctg dəyərləri bir-birinin əksidir.

Y = qara x.
Tangens x = π/2 + πk-də y dəyərlərinə meyl edir, lakin heç vaxt onlara çatmır.
Tangentoidin ən kiçik müsbət dövrü π-dir.
Tg (- x) = - tg x, yəni funksiya təkdir.
Tg x = 0, x = πk üçün.
Funksiya artır.
Tg x › 0, x ϵ üçün (πk, π/2 + πk).
Tg x ‹ 0, x ϵ üçün (— π/2 + πk, πk).
Törəmə (tg x)’ = 1/cos 2 ⁡x.

Mətndə aşağıdakı kotangentoidin qrafik şəklini nəzərdən keçirin.

Kotangentoidlərin əsas xüsusiyyətləri:

Y = çarpayı x.
Sinus və kosinus funksiyalarından fərqli olaraq, tangentoiddə Y bütün həqiqi ədədlər çoxluğunun dəyərlərini qəbul edə bilər.
Kotangentoid x = πk-də y dəyərlərinə meyl edir, lakin heç vaxt onlara çatmır.
Kotangentoidin ən kiçik müsbət dövrü π-dir.
Ctg (- x) = - ctg x, yəni funksiya təkdir.
Ctg x = 0, x = π/2 + πk üçün.
Funksiya azalır.
Ctg x › 0, x ϵ üçün (πk, π/2 + πk).
Ctg x ‹ 0, x ϵ üçün (π/2 + πk, πk).
Törəmə (ctg x)’ = - 1/sin 2 ⁡x Düzgün

Məqalədə bunun nəyə bənzədiyini tam başa düşəcəyik triqonometrik qiymətlər cədvəli, sinus, kosinus, tangens və kotangens. Triqonometrik funksiyaların əsas mənasını 0,30,45,60,90,...,360 dərəcə bucaqdan nəzərdən keçirək. Və gəlin triqonometrik funksiyaların qiymətlərini hesablamaqda bu cədvəllərdən necə istifadə edəcəyimizi görək.
Əvvəlcə baxaq kosinus, sinus, tangens və kotangens cədvəli 0, 30, 45, 60, 90,... dərəcə bucaqdan. Bu kəmiyyətlərin tərifi 0 və 90 dərəcə bucaqların funksiyalarının dəyərini təyin etməyə imkan verir:

sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, 00-dan kotangens təyin olunmayacaq
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0-dan tangens qeyri-müəyyən olacaq

Bucaqları 30 ilə 90 dərəcə arasında olan düzbucaqlı üçbucaqları götürsəniz. Biz əldə edirik:

sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, çarpayı 60 0 = √3/3

Bütün əldə edilən dəyərləri formada təmsil edək triqonometrik cədvəl:

Sinuslar, kosinuslar, tangenslər və kotangentlər cədvəli!

Azaltma düsturundan istifadə etsək, cədvəlimiz 360 dərəcəyə qədər bucaqlar üçün dəyərlər əlavə edərək artacaq. Bu kimi görünəcək:

Həmçinin dövriliyin xassələrinə əsaslanaraq bucaqları 0 0 +360 0 *z .... 330 0 +360 0 *z ilə əvəz etsək cədvəli artırmaq olar, burada z tam ədəddir. Bu cədvəldə bir dairədəki nöqtələrə uyğun gələn bütün bucaqların qiymətini hesablamaq mümkündür.

Cədvəlin həllində necə istifadə olunacağına baxaq.
Hər şey çox sadədir. Bizə lazım olan dəyər ehtiyac duyduğumuz hüceyrələrin kəsişmə nöqtəsində olduğundan. Məsələn, 60 dərəcə bucağın cosunu götürün, cədvəldə belə görünəcək:

Triqonometrik funksiyaların əsas dəyərlərinin yekun cədvəlində eyni şəkildə davam edirik. Amma bu cədvəldə 1020 dərəcə bucaqdan olan tangensin nə qədər olduğunu öyrənmək olar, bu = -√3 1020 0 = 300 0 +360 0 *2 yoxlayaq. Cədvəldən istifadə edərək onu tapaq.

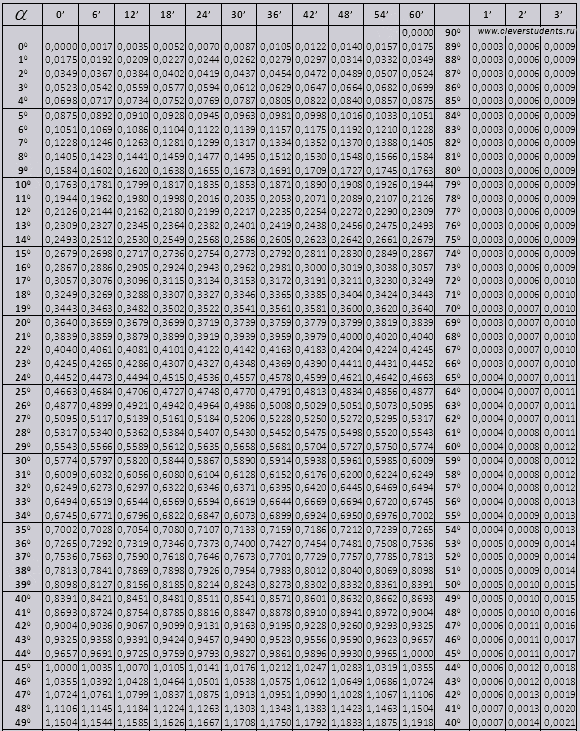
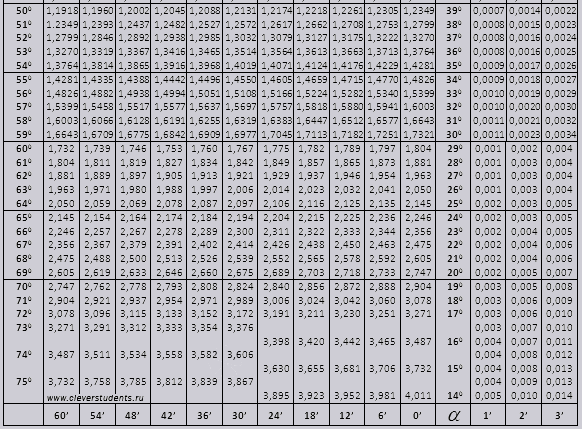
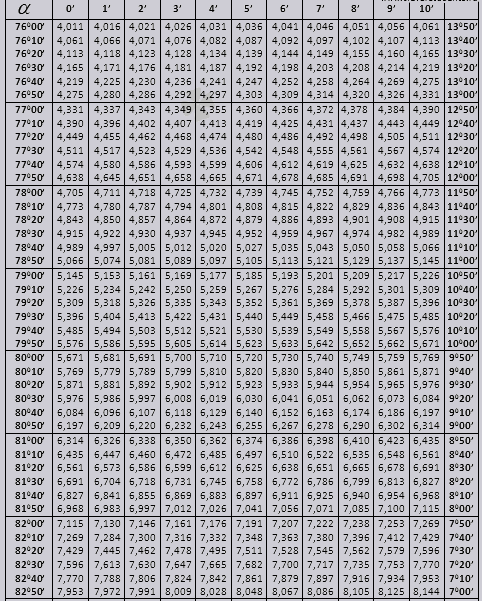
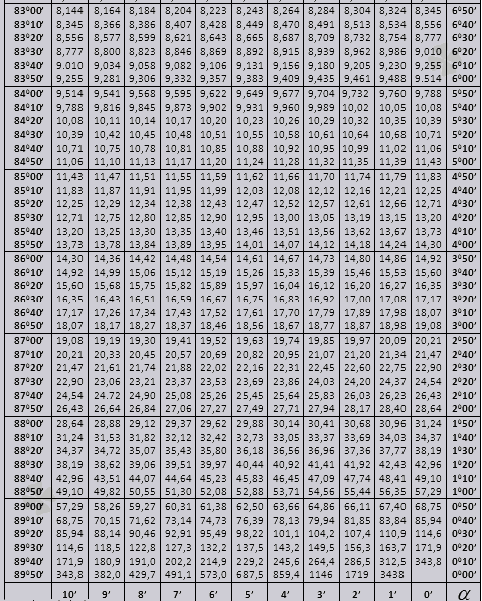
Bradis masası. Sinus, kosinus, tangens və kotangens üçün.

Bradis cədvəlləri iki hissəyə (90 dərəcəyə qədər bucaqların tg və kiçik bucaqların ctg) bölündüyü kosinus və sinus, tangens və kotangens cədvəllərindən ibarət bir neçə hissəyə bölünür.

Sinus və kosinus

tg bucaq 00-dan başlayan 760 ilə bitən, ctg 140 ilə başlayan 900 ilə bitən bucaq.

tg-ə qədər 900 və ctg kiçik açılar.

Gəlin problemlərin həllində Bradis cədvəllərindən necə istifadə edəcəyimizi anlayaq.

Sin təyinatını tapaq (sol kənardakı sütunda təyinat) 42 dəqiqə (təyinat yuxarı sətirdədir). Kəsişmə ilə təyinatı axtarırıq, = 0.3040.

Dəqiqə dəyərləri altı dəqiqəlik bir fasilə ilə göstərilir, ehtiyac duyduğumuz dəyər tam olaraq bu intervala düşərsə nə etməli. Gəlin 44 dəqiqə çəkək, amma cədvəldə cəmi 42 var.Biz 42-ni əsas götürüb sağ tərəfdəki əlavə sütunlardan istifadə edirik, 2-ci düzəlişi götürüb 0,3040 + 0,0006-ya əlavə edirik, 0,3046 alırıq.

Günah 47 dəqiqə ilə biz 48 dəqiqə əsas götürürük və ondan 1 düzəliş çıxarırıq, yəni 0,3057 - 0,0003 = 0,3054

Cos hesablayarkən, biz günaha bənzər şəkildə işləyirik, yalnız cədvəlin alt sırasını əsas götürürük. Məsələn, cos 20 0 = 0,9397

90 0-a qədər tg bucağının və kiçik bucağın çarpayısının dəyərləri düzgündür və onlarda heç bir düzəliş yoxdur. Məsələn, tg 78 0 37min = 4,967 tapın

və ctg 20 0 13min = 25,83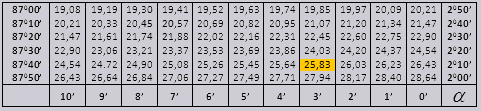

Yaxşı, biz əsas triqonometrik cədvəllərə baxdıq. Ümid edirik ki, bu məlumat sizin üçün çox faydalı oldu. Cədvəllərlə bağlı hər hansı bir sualınız varsa, şərhlərdə yazmağınızdan əmin olun!

Qeyd: Divar bamperləri divarları qorumaq üçün bamper lövhəsidir. Çərçivəsiz divar bamperləri linkini izləyin (http://www.spi-polymer.ru/otboyniki/) və daha çox məlumat əldə edin.

Bir nöqtədə mərkəzləşdirilmişdir A.
α - radyanla ifadə olunan bucaq.

Tərif
Sinus (sin α) düzbucaqlı üçbucağın hipotenuzası ilə ayağı arasındakı α bucağından asılı olaraq qarşı ayağın uzunluğunun nisbətinə bərabər olan triqonometrik funksiyadır |BC| hipotenuzanın uzunluğuna |AC|.

Kosinus (cos α) düzbucaqlı üçbucağın hipotenuzası ilə ayağı arasındakı α bucağından asılı olaraq bitişik ayağın uzunluğunun nisbətinə bərabər olan triqonometrik funksiyadır |AB| hipotenuzanın uzunluğuna |AC|.

Qəbul edilmiş qeydlər

;
;
.

Sinus funksiyasının qrafiki, y = sin x

Kosinus funksiyasının qrafiki, y = cos x

Sinus və kosinusun xassələri

Dövrilik

Funksiyalar y = günah x və y = cos x dövri ilə dövri 2π.

Paritet

Sinus funksiyası qəribədir. Kosinus funksiyası cütdür.

Tərif və dəyərlər sahəsi, ekstremal, artım, azalma

Sinus və kosinus funksiyaları öz tərif sahəsində davamlıdır, yəni bütün x üçün (davamlılığın sübutuna bax). Onların əsas xassələri cədvəldə verilmişdir (n - tam ədəd).

	y = günah x	y = cos x
Əhatə dairəsi və davamlılıq	- ∞ < x < + ∞	- ∞ < x < + ∞
Dəyərlər diapazonu	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Artan
Azalan
Maksimum, y = 1
Minimum, y = - 1
Sıfırlar, y = 0
Ordinat oxu ilə kəsişən nöqtələr, x = 0	y = 0	y = 1

Əsas düsturlar

Sinus və kosinusun kvadratlarının cəmi

Cəm və fərqdən sinus və kosinus üçün düsturlar

;
;

Sinusların və kosinusların hasilinin düsturları

Cəm və fərq düsturları

Kosinus vasitəsilə sinus ifadəsi

;
;
;
.

Kosinusu sinus vasitəsilə ifadə etmək

;
;
;
.

Tangens vasitəsilə ifadə

; .

Nə vaxt, bizdə:
; .

Burada:
; .

Sinuslar və kosinuslar, tangenslər və kotangentlər cədvəli

Bu cədvəl arqumentin müəyyən dəyərləri üçün sinus və kosinusların dəyərlərini göstərir.

Mürəkkəb dəyişənlər vasitəsilə ifadələr

;

Eyler düsturu

Hiperbolik funksiyalar vasitəsilə ifadələr

;
;

Törəmələri

; . Düsturların alınması > > >

n-ci dərəcəli törəmələr:
{ -∞ < x < +∞ }

Sekant, kosekant

Tərs funksiyalar

Sinus və kosinusun tərs funksiyaları müvafiq olaraq arksinüs və arkkosindir.

Arksin, arksin

Arkkosin, arkkos

İstinadlar:
İ.N. Bronstein, K.A. Semendyaev, Mühəndislər və kollec tələbələri üçün riyaziyyat kitabçası, "Lan", 2009.