Συνημίτονο 30 σύμφωνα με τον πίνακα Bradis. Ημίτονο (sin x) και συνημίτονο (cos x) – ιδιότητες, γραφήματα, τύποι

Πίνακας βασικών τριγωνομετρικών συναρτήσεων για γωνίες 0, 30, 45, 60, 90, ... μοιρών

Από τους τριγωνομετρικούς ορισμούς των συναρτήσεων $\sin$, $\cos$, $\tan$ και $\cot$, μπορείτε να μάθετε τις τιμές τους για τις γωνίες $0$ και $90$ μοίρες:

$\sin⁡0°=0$, $\cos0°=1$, $\tan 0°=0$, $\cot 0°$ δεν έχει οριστεί.

$\sin90°=1$, $\cos90°=0$, $\cot90°=0$, $\tan 90°$ δεν έχει προσδιοριστεί.

Σε ένα σχολικό μάθημα γεωμετρίας, όταν μελετάμε ορθογώνια τρίγωνα, βρίσκουμε τις τριγωνομετρικές συναρτήσεις των γωνιών $0°$, $30°$, $45°$, $60°$ και $90°$.

Βρέθηκαν τιμές τριγωνομετρικών συναρτήσεων για τις υποδεικνυόμενες γωνίες σε μοίρες και ακτίνια, αντίστοιχα ($0$, $\frac(\pi)(6)$, $\frac(\pi)(4)$, $\frac(\ pi)(3) $, $\frac(\pi)(2)$) για ευκολία απομνημόνευσης και χρήσης εισάγονται σε έναν πίνακα που ονομάζεται τριγωνομετρικός πίνακας, πίνακας βασικών τιμών τριγωνομετρικών συναρτήσεωνκαι ούτω καθεξής.

Όταν χρησιμοποιείτε τύπους μείωσης, ο τριγωνομετρικός πίνακας μπορεί να επεκταθεί σε γωνία $360°$ και, κατά συνέπεια, $2\pi$ ακτίνια:

Χρησιμοποιώντας τις ιδιότητες περιοδικότητας των τριγωνομετρικών συναρτήσεων, κάθε γωνία, η οποία θα διαφέρει από την ήδη γνωστή κατά $360°$, μπορεί να υπολογιστεί και να καταγραφεί σε έναν πίνακα. Για παράδειγμα, η τριγωνομετρική συνάρτηση για τη γωνία $0°$ θα έχει την ίδια τιμή για τη γωνία $0°+360°$ και για τη γωνία $0°+2 \cdot 360°$ και για τη γωνία $0°+3 \cdot 360°$ και τα λοιπά.

Χρησιμοποιώντας έναν τριγωνομετρικό πίνακα, μπορείτε να προσδιορίσετε τις τιμές όλων των γωνιών ενός κύκλου μονάδας.

Σε ένα μάθημα σχολικής γεωμετρίας, υποτίθεται ότι απομνημονεύετε τις βασικές τιμές των τριγωνομετρικών συναρτήσεων που συλλέγονται σε έναν τριγωνομετρικό πίνακα για την ευκολία επίλυσης τριγωνομετρικών προβλημάτων.

Χρησιμοποιώντας έναν πίνακα

Στον πίνακα, αρκεί να βρούμε την απαιτούμενη τριγωνομετρική συνάρτηση και την τιμή της γωνίας ή των ακτίνων για την οποία πρέπει να υπολογιστεί αυτή η συνάρτηση. Στην τομή της γραμμής με τη συνάρτηση και της στήλης με την τιμή, λαμβάνουμε την επιθυμητή τιμή της τριγωνομετρικής συνάρτησης του δεδομένου ορίσματος.

Στο σχήμα μπορείτε να δείτε πώς να βρείτε την τιμή του $\cos⁡60°$, που ισούται με $\frac(1)(2)$.

Ο εκτεταμένος τριγωνομετρικός πίνακας χρησιμοποιείται με τον ίδιο τρόπο. Το πλεονέκτημα της χρήσης του είναι, όπως ήδη αναφέρθηκε, ο υπολογισμός της τριγωνομετρικής συνάρτησης σχεδόν κάθε γωνίας. Για παράδειγμα, μπορείτε εύκολα να βρείτε την τιμή $\tan 1 380°=\tan (1 380°-360°)=\tan(1 020°-360°)=\tan(660°-360°)=\tan300 °$:

Πίνακες Bradis βασικών τριγωνομετρικών συναρτήσεων

Η δυνατότητα υπολογισμού της τριγωνομετρικής συνάρτησης απολύτως οποιασδήποτε τιμής γωνίας για ακέραια τιμή μοιρών και ακέραια τιμή λεπτών παρέχεται με τη χρήση πινάκων Bradis. Για παράδειγμα, βρείτε την τιμή του $\cos⁡34°7"$. Οι πίνακες χωρίζονται σε 2 μέρη: έναν πίνακα τιμών των $\sin$ και $\cos$ και έναν πίνακα τιμών των $ \tan$ και $\cot$.

Οι πίνακες Bradis καθιστούν δυνατή τη λήψη κατά προσέγγιση τιμών τριγωνομετρικών συναρτήσεων με ακρίβεια έως και 4 δεκαδικών ψηφίων.

Χρήση πινάκων Bradis

Χρησιμοποιώντας τους πίνακες Bradis για ημίτονο, βρίσκουμε $\sin⁡17°42"$. Για να το κάνετε αυτό, στην αριστερή στήλη του πίνακα ημιτόνων και συνημιτόνων βρίσκουμε την τιμή των μοιρών - $17°$ και στην επάνω γραμμή βρίσκουμε την τιμή των λεπτών - $42"$. Στη διασταύρωση τους παίρνουμε την επιθυμητή τιμή:

$\sin17°42"=0,304$.

Για να βρείτε την τιμή $\sin17°44"$ πρέπει να χρησιμοποιήσετε τη διόρθωση στη δεξιά πλευρά του πίνακα. Σε αυτήν την περίπτωση, στην τιμή $42"$, που βρίσκεται στον πίνακα, πρέπει να προσθέσετε μια διόρθωση για $2 "$, που ισούται με 0,0006$. Παίρνουμε:

$\sin17°44"=0,304+0,0006=0,3046$.

Για να βρούμε την τιμή $\sin17°47"$ χρησιμοποιούμε επίσης τη διόρθωση στη δεξιά πλευρά του πίνακα, μόνο σε αυτήν την περίπτωση παίρνουμε ως βάση την τιμή $\sin17°48"$ και αφαιρούμε τη διόρθωση για $1"$ :

$\sin17°47"=0,3057-0,0003=0,3054$.

Κατά τον υπολογισμό των συνημίτονων, εκτελούμε παρόμοιες ενέργειες, αλλά κοιτάμε τις μοίρες στη δεξιά στήλη και τα λεπτά στην κάτω στήλη του πίνακα. Για παράδειγμα, $\cos20°=0,9397$.

Δεν υπάρχουν διορθώσεις για τιμές εφαπτομένης έως $90°$ και μικρής γωνίας συνεφαπτομένης. Για παράδειγμα, ας βρούμε $\tan 78°37"$, που σύμφωνα με τον πίνακα ισούται με $4,967 $.

ΠΙΝΑΚΑΣ ΤΙΜΩΝ ΤΡΙΓΩΝΟΜΕΤΡΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ

Ο πίνακας τιμών των τριγωνομετρικών συναρτήσεων καταρτίζεται για γωνίες 0, 30, 45, 60, 90, 180, 270 και 360 μοιρών και τις αντίστοιχες τιμές γωνίας σε βράδια. Από τις τριγωνομετρικές συναρτήσεις, ο πίνακας δείχνει ημίτονο, συνημίτονο, εφαπτομένη, συνεφαπτομένη, τέμνουσα και συνημίτονο. Για τη διευκόλυνση της επίλυσης σχολικών παραδειγμάτων, οι τιμές των τριγωνομετρικών συναρτήσεων στον πίνακα γράφονται με τη μορφή κλάσματος, ενώ διατηρούνται τα σημάδια για την εξαγωγή της τετραγωνικής ρίζας των αριθμών, κάτι που πολύ συχνά βοηθά στη μείωση σύνθετων μαθηματικών παραστάσεων. Για την εφαπτομένη και την συνεφαπτομένη, οι τιμές ορισμένων γωνιών δεν μπορούν να προσδιοριστούν. Για τις τιμές της εφαπτομένης και της συνεφαπτομένης τέτοιων γωνιών, υπάρχει μια παύλα στον πίνακα τιμών των τριγωνομετρικών συναρτήσεων. Είναι γενικά αποδεκτό ότι η εφαπτομένη και η συνεφαπτομένη τέτοιων γωνιών είναι ίση με το άπειρο. Σε ξεχωριστή σελίδα υπάρχουν τύποι για τη μείωση των τριγωνομετρικών συναρτήσεων.

Ο πίνακας τιμών για τη συνάρτηση τριγωνομετρικού ημιτόνου δείχνει τις τιμές για τις ακόλουθες γωνίες: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 σε μοίρες, που αντιστοιχεί σε sin 0 pi, sin pi/6 , sin pi/4, sin pi/3, sin pi/2, sin pi, sin 3 pi/2, sin 2 pi σε ακτινική μέτρηση γωνιών. Σχολικός πίνακας ημιτόνων.

Για την τριγωνομετρική συνάρτηση συνημιτόνου, ο πίνακας δείχνει τις τιμές για τις ακόλουθες γωνίες: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 σε μοίρες, που αντιστοιχεί σε cos 0 pi , cos pi κατά 6, cos pi κατά 4, cos pi κατά 3, cos pi κατά 2, cos pi, cos 3 pi επί 2, cos 2 pi σε ακτινική μέτρηση γωνιών. Σχολικός πίνακας συνημίτονων.

Ο τριγωνομετρικός πίνακας για τη συνάρτηση τριγωνομετρικής εφαπτομένης δίνει τιμές για τις ακόλουθες γωνίες: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 σε μοίρες, που αντιστοιχεί σε tg 0 pi, tg pi/6, tg pi/4, tg pi/3, tg pi, tg 2 pi σε ακτινική μέτρηση γωνιών. Οι ακόλουθες τιμές των τριγωνομετρικών συναρτήσεων εφαπτομένης δεν ορίζονται tan 90, tan 270, tan pi/2, tan 3 pi/2 και θεωρούνται ίσες με το άπειρο.

Για την τριγωνομετρική συνάρτηση συνεφαπτομένη στον τριγωνομετρικό πίνακα δίνονται οι τιμές των ακόλουθων γωνιών: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 σε μέτρο μοιρών, που αντιστοιχεί σε ctg pi/6, ctg pi/4 , ctg pi/3, tg pi/ 2, tan 3 pi/2 σε ακτινική μέτρηση γωνιών. Οι ακόλουθες τιμές των τριγωνομετρικών συναρτήσεων συνεφαπτομένης δεν ορίζονται ctg 0, ctg 180, ctg 360, ctg 0 pi, ctg pi, ctg 2 pi και θεωρούνται ίσες με το άπειρο.

Οι τιμές των τριγωνομετρικών συναρτήσεων τέμνουσα και συνεφαπτομένη δίνονται για τις ίδιες γωνίες σε μοίρες και ακτίνια με το ημίτονο, συνημίτονο, εφαπτομένη, συνεφαπτομένη.

Ο πίνακας τιμών των τριγωνομετρικών συναρτήσεων μη τυπικών γωνιών δείχνει τις τιμές του ημιτόνου, του συνημιτόνου, της εφαπτομένης και της συνεφαπτομένης για γωνίες σε μοίρες 15, 18, 22,5, 36, 54, 67,5 72 μοίρες και σε ακτίνια pi/12 , pi/10, pi/ 8, pi/5, 3pi/8, 2pi/5 ακτίνια. Οι τιμές των τριγωνομετρικών συναρτήσεων εκφράζονται σε κλάσματα και τετραγωνικές ρίζες για να διευκολύνεται η μείωση των κλασμάτων στα σχολικά παραδείγματα.

Τρία ακόμη τέρατα τριγωνομετρίας. Το πρώτο είναι η εφαπτομένη του 1,5 μιάμιση μοίρα ή π διαιρούμενο με το 120. Το δεύτερο είναι το συνημίτονο του π διαιρούμενο με το 240, pi/240. Το μεγαλύτερο είναι το συνημίτονο του pi διαιρούμενο με το 17, pi/17.

Ο τριγωνομετρικός κύκλος των τιμών των συναρτήσεων ημιτονοειδές και συνημίτονο αναπαριστά οπτικά τα σημάδια του ημιτονοειδούς και του συνημιτόνου ανάλογα με το μέγεθος της γωνίας. Ειδικά για τις ξανθιές, οι τιμές συνημιτόνου υπογραμμίζονται με μια πράσινη παύλα για να μειωθεί η σύγχυση. Η μετατροπή των μοιρών σε ακτίνια παρουσιάζεται επίσης πολύ καθαρά όταν τα ακτίνια εκφράζονται σε pi.

Αυτός ο τριγωνομετρικός πίνακας παρουσιάζει τις τιμές του ημιτόνου, του συνημιτόνου, της εφαπτομένης και της συνεφαπτομένης για γωνίες από 0 μηδέν έως 90 ενενήντα μοίρες σε διαστήματα μιας μοίρας. Για τις πρώτες σαράντα πέντε μοίρες, τα ονόματα των τριγωνομετρικών συναρτήσεων θα πρέπει να εξετάζονται στην κορυφή του πίνακα. Η πρώτη στήλη περιέχει μοίρες, οι τιμές των ημιτόνων, των συνημιτόνων, των εφαπτομένων και των συνεφαπτομένων αναγράφονται στις επόμενες τέσσερις στήλες.

Για γωνίες από σαράντα πέντε μοίρες έως ενενήντα μοίρες, τα ονόματα των τριγωνομετρικών συναρτήσεων αναγράφονται στο κάτω μέρος του πίνακα. Η τελευταία στήλη περιέχει μοίρες· οι τιμές των συνημιτόνων, των ημιτόνων, των συνεφαπτομένων και των εφαπτομένων αναγράφονται στις προηγούμενες τέσσερις στήλες. Θα πρέπει να είστε προσεκτικοί γιατί τα ονόματα των τριγωνομετρικών συναρτήσεων στο κάτω μέρος του τριγωνομετρικού πίνακα είναι διαφορετικά από τα ονόματα στην κορυφή του πίνακα. Τα ημιτόνια και τα συνημίτονα ανταλλάσσονται, όπως η εφαπτομένη και η συνεφαπτομένη. Αυτό οφείλεται στη συμμετρία των τιμών των τριγωνομετρικών συναρτήσεων.

Τα σημάδια των τριγωνομετρικών συναρτήσεων φαίνονται στο παραπάνω σχήμα. Το ημίτονο έχει θετικές τιμές από 0 έως 180 μοίρες ή από 0 έως pi. Το ημίτονο έχει αρνητικές τιμές από 180 έως 360 μοίρες ή από pi έως 2 pi. Οι τιμές συνημιτόνου είναι θετικές από 0 έως 90 και 270 έως 360 μοίρες ή 0 έως 1/2 pi και 3/2 έως 2 pi. Η εφαπτομένη και η συνεφαπτομένη έχουν θετικές τιμές από 0 έως 90 μοίρες και από 180 έως 270 μοίρες, που αντιστοιχούν σε τιμές από 0 έως 1/2 pi και pi έως 3/2 pi. Οι αρνητικές τιμές της εφαπτομένης και της συνεφαπτομένης είναι από 90 έως 180 μοίρες και από 270 έως 360 μοίρες ή από 1/2 pi έως pi και από 3/2 pi έως 2 pi. Όταν προσδιορίζετε τα σημάδια των τριγωνομετρικών συναρτήσεων για γωνίες μεγαλύτερες από 360 μοίρες ή 2 pi, θα πρέπει να χρησιμοποιείτε τις ιδιότητες περιοδικότητας αυτών των συναρτήσεων.

Οι τριγωνομετρικές συναρτήσεις ημίτονο, εφαπτομένη και συνεφαπτομένη είναι περιττές συναρτήσεις. Οι τιμές αυτών των συναρτήσεων για αρνητικές γωνίες θα είναι αρνητικές. Το συνημίτονο είναι μια άρτια τριγωνομετρική συνάρτηση - η τιμή του συνημιτόνου για μια αρνητική γωνία θα είναι θετική. Κατά τον πολλαπλασιασμό και τη διαίρεση τριγωνομετρικών συναρτήσεων πρέπει να τηρούνται οι κανόνες πρόσημου.

Ο πίνακας τιμών για τη συνάρτηση τριγωνομετρικού ημιτόνου δείχνει τις τιμές για τις ακόλουθες γωνίες
Εγγραφο
Υπάρχουν τύποι μείωσης σε ξεχωριστή σελίδα τριγωνομετρικήλειτουργίες. ΣΕ τραπέζιαξίεςΓιατριγωνομετρικήλειτουργίεςκόλποςδεδομένοςαξίεςΓιατο ακόλουθογωνίες: αμαρτία 0, αμαρτία 30, αμαρτία 45 ...
Η προτεινόμενη μαθηματική συσκευή είναι ένα πλήρες ανάλογο μιγαδικού λογισμού για ν-διάστατους υπερσύνθετους αριθμούς με οποιονδήποτε αριθμό βαθμών ελευθερίας n και προορίζεται για μαθηματική μοντελοποίηση μη γραμμικών
Εγγραφο
... λειτουργίεςισοδυναμεί λειτουργίεςεικόνες. Από αυτό το θεώρημα πρέπει, Τι Γιαβρίσκοντας τις συντεταγμένες U, V, αρκεί να υπολογίσουμε λειτουργία... γεωμετρία? πολυνερ λειτουργίες(πολυδιάστατα ανάλογα δισδιάστατων τριγωνομετρικήλειτουργίες), τις ιδιότητες τους, τραπέζιακαι εφαρμογή? ...

Η τριγωνομετρία, ως επιστήμη, ξεκίνησε από την Αρχαία Ανατολή. Οι πρώτες τριγωνομετρικές αναλογίες προήλθαν από αστρονόμους για να δημιουργήσουν ένα ακριβές ημερολόγιο και προσανατολισμό από τα αστέρια. Οι υπολογισμοί αυτοί αφορούσαν τη σφαιρική τριγωνομετρία, ενώ στο σχολικό μάθημα μελετούν τον λόγο πλευρών και γωνιών ενός επιπέδου τριγώνου.

Η τριγωνομετρία είναι ένας κλάδος των μαθηματικών που ασχολείται με τις ιδιότητες των τριγωνομετρικών συναρτήσεων και τις σχέσεις μεταξύ των πλευρών και των γωνιών των τριγώνων.

Κατά την ακμή του πολιτισμού και της επιστήμης την 1η χιλιετία μ.Χ., η γνώση εξαπλώθηκε από την Αρχαία Ανατολή στην Ελλάδα. Αλλά οι κύριες ανακαλύψεις της τριγωνομετρίας είναι η αξία των ανδρών του Αραβικού Χαλιφάτου. Συγκεκριμένα, ο Τουρκμενός επιστήμονας al-Marazwi εισήγαγε συναρτήσεις όπως η εφαπτομένη και η συνεφαπτομένη και συνέταξε τους πρώτους πίνακες τιμών για ημιτονοειδή, εφαπτομένες και συνεφαπτομένες. Οι έννοιες του ημιτόνου και του συνημιτονοειδούς εισήχθησαν από Ινδούς επιστήμονες. Η τριγωνομετρία έλαβε μεγάλη προσοχή στα έργα μεγάλων μορφών της αρχαιότητας όπως ο Ευκλείδης, ο Αρχιμήδης και ο Ερατοσθένης.

Βασικά μεγέθη τριγωνομετρίας

Οι βασικές τριγωνομετρικές συναρτήσεις ενός αριθμητικού ορίσματος είναι το ημίτονο, το συνημίτονο, η εφαπτομένη και η συνεφαπτομένη. Κάθε ένα από αυτά έχει το δικό του γράφημα: ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη.

Οι τύποι για τον υπολογισμό των τιμών αυτών των μεγεθών βασίζονται στο Πυθαγόρειο θεώρημα. Είναι πιο γνωστό στους μαθητές στη διατύπωση: «Τα πυθαγόρεια παντελόνια είναι ίσα προς όλες τις κατευθύνσεις», αφού η απόδειξη δίνεται χρησιμοποιώντας το παράδειγμα ενός ισοσκελούς ορθογωνίου τριγώνου.

Το ημίτονο, το συνημίτονο και άλλες σχέσεις καθορίζουν τη σχέση μεταξύ των οξειών γωνιών και πλευρών οποιουδήποτε ορθογωνίου τριγώνου. Ας παρουσιάσουμε τύπους για τον υπολογισμό αυτών των μεγεθών για τη γωνία Α και ας ανιχνεύσουμε τις σχέσεις μεταξύ τριγωνομετρικών συναρτήσεων:

Όπως μπορείτε να δείτε, το tg και το ctg είναι αντίστροφες συναρτήσεις. Αν φανταστούμε το σκέλος a ως γινόμενο της αμαρτίας Α και της υποτείνουσας c και το σκέλος b ως cos A * c, λαμβάνουμε τους ακόλουθους τύπους για την εφαπτομένη και την συνεφαπτομένη:

Τριγωνομετρικός κύκλος

Γραφικά, η σχέση μεταξύ των αναφερόμενων ποσοτήτων μπορεί να αναπαρασταθεί ως εξής:

Ο κύκλος, σε αυτή την περίπτωση, αντιπροσωπεύει όλες τις πιθανές τιμές της γωνίας α - από 0° έως 360°. Όπως φαίνεται από το σχήμα, κάθε συνάρτηση παίρνει μια αρνητική ή θετική τιμή ανάλογα με τη γωνία. Για παράδειγμα, το sin α θα έχει πρόσημο «+» αν το α ανήκει στο 1ο και το 2ο τέταρτο του κύκλου, δηλαδή είναι στην περιοχή από 0° έως 180°. Για α από 180° έως 360° (ΙΙΙ και IV τέταρτα), το sin α μπορεί να είναι μόνο αρνητική τιμή.

Ας προσπαθήσουμε να φτιάξουμε τριγωνομετρικούς πίνακες για συγκεκριμένες γωνίες και να μάθουμε τη σημασία των μεγεθών.

Οι τιμές του α ίσες με 30°, 45°, 60°, 90°, 180° και ούτω καθεξής ονομάζονται ειδικές περιπτώσεις. Οι τιμές των τριγωνομετρικών συναρτήσεων για αυτές υπολογίζονται και παρουσιάζονται με τη μορφή ειδικών πινάκων.

Αυτές οι γωνίες δεν επιλέχθηκαν τυχαία. Ο προσδιορισμός π στους πίνακες είναι για ακτίνια. Rad είναι η γωνία στην οποία το μήκος του τόξου ενός κύκλου αντιστοιχεί στην ακτίνα του. Αυτή η τιμή εισήχθη για να δημιουργηθεί μια καθολική εξάρτηση· κατά τον υπολογισμό σε ακτίνια, το πραγματικό μήκος της ακτίνας σε cm δεν έχει σημασία.

Οι γωνίες σε πίνακες για τριγωνομετρικές συναρτήσεις αντιστοιχούν σε τιμές ακτίνων:

Έτσι, δεν είναι δύσκολο να μαντέψει κανείς ότι το 2π είναι ένας πλήρης κύκλος ή 360°.

Ιδιότητες τριγωνομετρικών συναρτήσεων: ημίτονο και συνημίτονο

Προκειμένου να εξεταστούν και να συγκριθούν οι βασικές ιδιότητες του ημιτόνου και του συνημιτονοειδούς, της εφαπτομένης και της συνεφαπτομένης, είναι απαραίτητο να σχεδιάσουμε τις συναρτήσεις τους. Αυτό μπορεί να γίνει με τη μορφή μιας καμπύλης που βρίσκεται σε ένα δισδιάστατο σύστημα συντεταγμένων.

Εξετάστε τον συγκριτικό πίνακα ιδιοτήτων για το ημίτονο και το συνημίτονο:

Ημιτονοειδές κύμα	Συνημίτονο
y = sinx	y = cos x
ODZ [-1; 1]	ODZ [-1; 1]
sin x = 0, για x = πk, όπου k ϵ Z	cos x = 0, για x = π/2 + πk, όπου k ϵ Z
sin x = 1, για x = π/2 + 2πk, όπου k ϵ Z	cos x = 1, σε x = 2πk, όπου k ϵ Z
sin x = - 1, στο x = 3π/2 + 2πk, όπου k ϵ Z	cos x = - 1, για x = π + 2πk, όπου k ϵ Z
sin (-x) = - sin x, δηλαδή η συνάρτηση είναι περιττή	cos (-x) = cos x, δηλαδή η συνάρτηση είναι άρτια
	η συνάρτηση είναι περιοδική, η μικρότερη περίοδος είναι 2π
sin x › 0, με το x να ανήκει στο 1ο και 2ο τέταρτο ή από 0° έως 180° (2πk, π + 2πk)	cos x › 0, με το x να ανήκει στο I και IV τέταρτο ή από 270° έως 90° (- π/2 + 2πk, π/2 + 2πk)
sin x ‹ 0, με το x να ανήκει στο τρίτο και τέταρτο τέταρτο ή από 180° έως 360° (π + 2πk, 2π + 2πk)	cos x ‹ 0, με το x να ανήκει στο 2ο και 3ο τέταρτο ή από 90° έως 270° (π/2 + 2πk, 3π/2 + 2πk)
αυξάνεται στο διάστημα [- π/2 + 2πk, π/2 + 2πk]	αυξάνεται στο διάστημα [-π + 2πk, 2πk]
μειώνεται κατά διαστήματα [π/2 + 2πk, 3π/2 + 2πk]	μειώνεται κατά διαστήματα
παράγωγο (sin x)’ = cos x	παράγωγο (cos x)’ = - sin x

Ο προσδιορισμός του αν μια συνάρτηση είναι άρτια ή όχι είναι πολύ απλός. Αρκεί να φανταστεί κανείς έναν τριγωνομετρικό κύκλο με τα σημάδια των τριγωνομετρικών μεγεθών και να «διπλώσει» νοερά το γράφημα σε σχέση με τον άξονα OX. Αν τα πρόσημα συμπίπτουν, η συνάρτηση είναι άρτια, διαφορετικά είναι περιττή.

Η εισαγωγή των ακτίνων και η απαρίθμηση των βασικών ιδιοτήτων των ημιτονοειδών και συνημιτονικών κυμάτων μας επιτρέπουν να παρουσιάσουμε το ακόλουθο μοτίβο:

Είναι πολύ εύκολο να επαληθεύσετε ότι ο τύπος είναι σωστός. Για παράδειγμα, για x = π/2, το ημίτονο είναι 1, όπως και το συνημίτονο του x = 0. Ο έλεγχος μπορεί να γίνει με τη συμβουλή πινάκων ή με τον εντοπισμό καμπυλών συναρτήσεων για δεδομένες τιμές.

Ιδιότητες εφαπτομενοειδών και συνεφαπτομένων

Τα γραφήματα των συναρτήσεων εφαπτομένης και συνεφαπτομένης διαφέρουν σημαντικά από τις συναρτήσεις ημιτονοειδούς και συνημιτονοειδούς. Οι τιμές tg και ctg είναι αμοιβαίες μεταξύ τους.

Y = tan x.
Η εφαπτομένη τείνει στις τιμές του y στο x = π/2 + πk, αλλά δεν τις φτάνει ποτέ.
Η μικρότερη θετική περίοδος της εφαπτομένης είναι το π.
Tg (- x) = - tg x, δηλαδή η συνάρτηση είναι περιττή.
Tg x = 0, για x = πk.
Η συνάρτηση αυξάνεται.
Tg x › 0, για x ϵ (πk, π/2 + πk).
Tg x ‹ 0, για x ϵ (— π/2 + πk, πk).
Παράγωγος (tg x)’ = 1/cos 2 ⁡x.

Εξετάστε τη γραφική εικόνα του συνεφαπτοειδούς παρακάτω στο κείμενο.

Βασικές ιδιότητες των κοτανγονοειδών:

Υ = κούνια x.
Σε αντίθεση με τις συναρτήσεις ημιτονοειδούς και συνημιτονοειδούς, στην εφαπτομενική Y μπορεί να λάβει τις τιμές του συνόλου όλων των πραγματικών αριθμών.
Το συνεφαπτοειδές τείνει στις τιμές του y στο x = πk, αλλά δεν τις φτάνει ποτέ.
Η μικρότερη θετική περίοδος ενός συνεφαπτοειδούς είναι το π.
Ctg (- x) = - ctg x, δηλαδή η συνάρτηση είναι περιττή.
Ctg x = 0, για x = π/2 + πk.
Η συνάρτηση μειώνεται.
Ctg x › 0, για x ϵ (πk, π/2 + πk).
Ctg x ‹ 0, για x ϵ (π/2 + πk, πk).
Παράγωγο (ctg x)’ = - 1/sin 2 ⁡x Σωστό

Στο άρθρο, θα καταλάβουμε πλήρως πώς μοιάζει πίνακας τριγωνομετρικών τιμών, ημιτόνου, συνημίτονος, εφαπτομένης και συνεφαπτομένης. Ας εξετάσουμε τη βασική έννοια των τριγωνομετρικών συναρτήσεων, από γωνία 0,30,45,60,90,...,360 μοιρών. Και ας δούμε πώς να χρησιμοποιήσουμε αυτούς τους πίνακες για τον υπολογισμό των τιμών των τριγωνομετρικών συναρτήσεων.
Πρώτα ας δούμε πίνακας συνημιτόνου, ημιτόνου, εφαπτομένης και συνεφαπτομένηςαπό γωνία 0, 30, 45, 60, 90,... μοιρών. Ο ορισμός αυτών των μεγεθών μας επιτρέπει να προσδιορίσουμε την τιμή των συναρτήσεων των γωνιών 0 και 90 μοιρών:

sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, η συνεφαπτομένη από 00 θα είναι απροσδιόριστη
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, η εφαπτομένη από 90 0 θα είναι αβέβαιη

Αν πάρετε ορθογώνια τρίγωνα των οποίων οι γωνίες είναι από 30 έως 90 μοίρες. Παίρνουμε:

sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
αμαρτία 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, κούνια 60 0 = √3/3

Ας αντιπροσωπεύσουμε όλες τις λαμβανόμενες τιμές στη φόρμα τριγωνομετρικός πίνακας:

Πίνακας ημιτόνων, συνημιτόνων, εφαπτομένων και συνεφαπτομένων!

Εάν χρησιμοποιήσουμε τον τύπο μείωσης, ο πίνακας μας θα αυξηθεί, προσθέτοντας τιμές για γωνίες έως 360 μοίρες. Θα μοιάζει με:

Επίσης, με βάση τις ιδιότητες της περιοδικότητας, ο πίνακας μπορεί να αυξηθεί αν αντικαταστήσουμε τις γωνίες με 0 0 +360 0 *z .... 330 0 +360 0 *z, όπου το z είναι ακέραιος. Σε αυτόν τον πίνακα είναι δυνατό να υπολογιστεί η τιμή όλων των γωνιών που αντιστοιχούν σε σημεία ενός μόνο κύκλου.

Ας δούμε πώς να χρησιμοποιήσετε τον πίνακα σε μια λύση.
Όλα είναι πολύ απλά. Επειδή η τιμή που χρειαζόμαστε βρίσκεται στο σημείο τομής των κελιών που χρειαζόμαστε. Για παράδειγμα, πάρτε το cos μιας γωνίας 60 μοιρών, στον πίνακα θα μοιάζει με:

Στον τελικό πίνακα των κύριων τιμών των τριγωνομετρικών συναρτήσεων, προχωράμε με τον ίδιο τρόπο. Αλλά σε αυτόν τον πίνακα είναι δυνατό να μάθουμε πόση είναι η εφαπτομένη από γωνία 1020 μοιρών, = -√3 Ας ελέγξουμε 1020 0 = 300 0 +360 0 *2. Ας το βρούμε χρησιμοποιώντας τον πίνακα.

Τραπέζι Bradis. Για ημίτονο, συνημίτονο, εφαπτομένη και συνεφαπτομένη.

Οι πίνακες Bradis χωρίζονται σε διάφορα μέρη, που αποτελούνται από πίνακες συνημιτόνου και ημιτονοειδούς, εφαπτομένης και συνεφαπτομένης - που χωρίζεται σε δύο μέρη (tg γωνιών έως 90 μοίρες και ctg μικρών γωνιών).

Ημίτονο και συνημίτονο

tg γωνίας που αρχίζει από 00 και τελειώνει με 760, ctg γωνίας που αρχίζει με 140 και τελειώνει με 900.

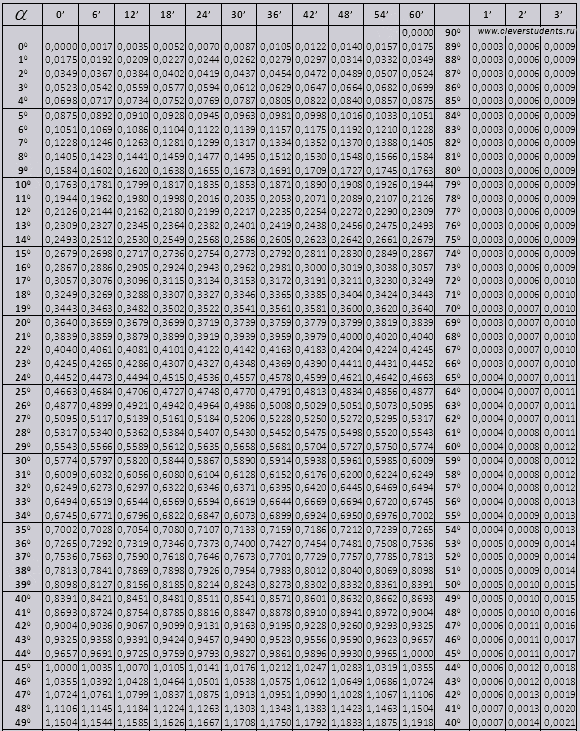
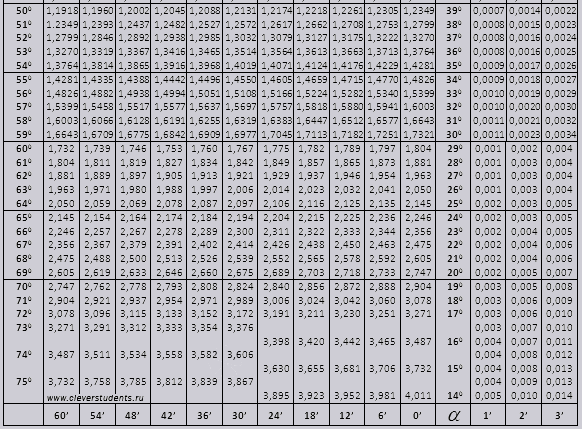
tg έως 900 και ctg μικρών γωνιών.

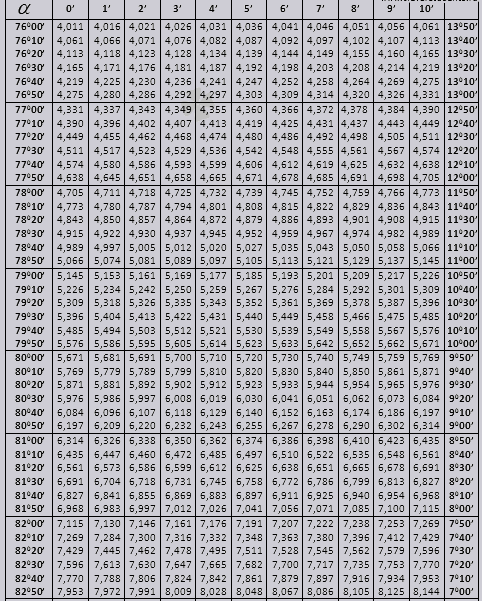
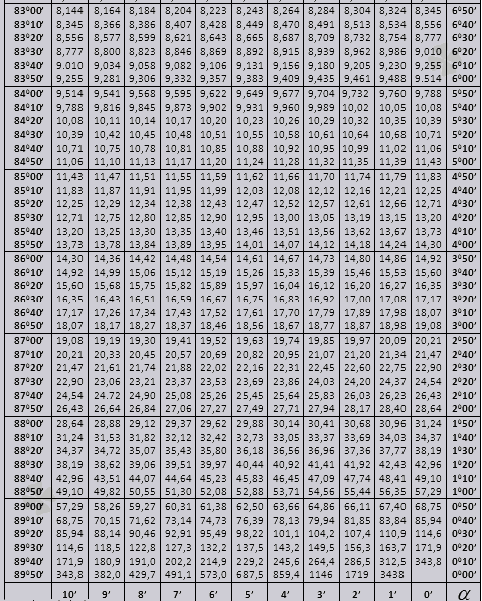
Ας μάθουμε πώς να χρησιμοποιήσουμε τους πίνακες Bradis στην επίλυση προβλημάτων.

Ας βρούμε τον προσδιορισμό αμαρτία (ονομασία στη στήλη στην αριστερή άκρη) 42 λεπτά (η ονομασία βρίσκεται στην επάνω γραμμή). Με τομή αναζητούμε τον προσδιορισμό, είναι = 0,3040.

Οι τιμές των λεπτών υποδεικνύονται με ένα διάστημα έξι λεπτών, τι πρέπει να κάνουμε εάν η τιμή που χρειαζόμαστε εμπίπτει ακριβώς σε αυτό το διάστημα. Ας πάρουμε 44 λεπτά, αλλά στον πίνακα υπάρχουν μόνο 42. Λαμβάνουμε ως βάση το 42 και χρησιμοποιούμε τις πρόσθετες στήλες στη δεξιά πλευρά, λαμβάνουμε τη 2η τροποποίηση και προσθέτουμε στο 0,3040 + 0,0006 παίρνουμε 0,3046.

Με αμαρτία 47 λεπτά, παίρνουμε ως βάση 48 λεπτά και αφαιρούμε 1 διόρθωση από αυτό, δηλαδή 0,3057 - 0,0003 = 0,3054

Κατά τον υπολογισμό του cos, εργαζόμαστε παρόμοια με το sin, μόνο που παίρνουμε ως βάση την κάτω σειρά του πίνακα. Για παράδειγμα cos 20 0 = 0,9397

Οι τιμές της γωνίας tg έως 90 0 και του κρεβατιού μικρής γωνίας είναι σωστές και δεν υπάρχουν διορθώσεις σε αυτές. Για παράδειγμα, βρείτε tg 78 0 37min = 4,967

και ctg 20 0 13min = 25,83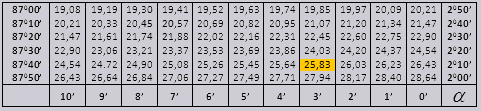

Λοιπόν, εξετάσαμε τους βασικούς τριγωνομετρικούς πίνακες. Ελπίζουμε ότι αυτές οι πληροφορίες ήταν εξαιρετικά χρήσιμες για εσάς. Αν έχετε απορίες σχετικά με τους πίνακες, γράψτε οπωσδήποτε στα σχόλια!

Σημείωση: Οι προφυλακτήρες τοίχου είναι μια σανίδα προφυλακτήρα για την προστασία των τοίχων. Ακολουθήστε τον σύνδεσμο προφυλακτήρες τοίχου χωρίς πλαίσιο (http://www.spi-polymer.ru/otboyniki/) και μάθετε περισσότερα.

Στο κέντρο σε ένα σημείο ΕΝΑ.
α - γωνία εκφρασμένη σε ακτίνια.

Ορισμός
Ημίτονος (αμαρτία α)είναι μια τριγωνομετρική συνάρτηση που εξαρτάται από τη γωνία α μεταξύ της υποτείνουσας και του σκέλους ενός ορθογωνίου τριγώνου, ίση με τον λόγο του μήκους του απέναντι σκέλους |BC| στο μήκος της υποτείνουσας |AC|.

συνημίτονο (συν α)είναι μια τριγωνομετρική συνάρτηση που εξαρτάται από τη γωνία α μεταξύ της υποτείνουσας και του σκέλους ενός ορθογωνίου τριγώνου, ίση με τον λόγο του μήκους του διπλανού σκέλους |AB| στο μήκος της υποτείνουσας |AC|.

Αποδεκτές σημειώσεις

;
;
.

Γράφημα της συνάρτησης ημιτόνου, y = sin x

Γράφημα της συνημίτονος, y = cos x

Ιδιότητες ημιτόνου και συνημιτόνου

Περιοδικότης

Συναρτήσεις y = αμαρτία xκαι y = cos xπεριοδική με περίοδο 2π.

Ισοτιμία

Η ημιτονοειδής συνάρτηση είναι περιττή. Η συνημίτονο είναι άρτια.

Τομέας ορισμού και τιμών, άκρα, αύξηση, μείωση

Οι συναρτήσεις ημιτονοειδούς και συνημιτονοειδούς είναι συνεχείς στο πεδίο ορισμού τους, δηλαδή για όλα τα x (βλ. απόδειξη συνέχειας). Οι κύριες ιδιότητές τους παρουσιάζονται στον πίνακα (n - ακέραιος).

	y = αμαρτία x	y = cos x
Πεδίο εφαρμογής και συνέχεια	- ∞ < x < + ∞	- ∞ < x < + ∞
Εύρος τιμών	-1 ≤ y ≤ 1	-1 ≤ y ≤ 1
Αυξάνεται
Φθίνων
Maxima, y = 1
Ελάχιστα, y = - 1
Μηδενικά, y = 0
Σημεία τομής με τον άξονα τεταγμένων, x = 0	y = 0	y = 1

Βασικοί τύποι

Άθροισμα τετραγώνων ημιτόνου και συνημιτόνου

Τύποι για ημίτονο και συνημίτονο από άθροισμα και διαφορά

;
;

Τύποι για το γινόμενο ημιτόνων και συνημιτόνων

Τύποι αθροίσματος και διαφοράς

Έκφραση ημιτόνου μέσω συνημίτονος

;
;
;
.

Έκφραση συνημιτόνου μέσω ημιτονοειδούς

;
;
;
.

Έκφραση μέσω της εφαπτομένης

; .

Όταν , έχουμε:
; .

Στο:
; .

Πίνακας ημιτόνων και συνημιτόνων, εφαπτομένων και συνεφαπτομένων

Αυτός ο πίνακας δείχνει τις τιμές των ημιτόνων και των συνημιτόνων για ορισμένες τιμές του ορίσματος.

Εκφράσεις μέσω μιγαδικών μεταβλητών

;

Ο τύπος του Euler

Εκφράσεις μέσω υπερβολικών συναρτήσεων

;
;

Παράγωγα

; . Εξαγωγή τύπων > > >

Παράγωγα νης τάξης:
{ -∞ < x < +∞ }

Secant, συνοδευτικό

Αντίστροφες συναρτήσεις

Οι αντίστροφες συναρτήσεις του ημιτόνου και του συνημίτονου είναι το τόξο και η αρκοσίνη, αντίστοιχα.

Arcsine, arcsin

Arccosine, arccos

Βιβλιογραφικές αναφορές:
ΣΕ. Bronstein, Κ.Α. Semendyaev, Εγχειρίδιο μαθηματικών για μηχανικούς και φοιτητές, "Lan", 2009.